На плоскости даны два отрезка АВ и CD. Найти геометрическое место точек М, обладающих тем свойством, что сумма площадей треугольников АМВ и CMD равна некоторой постоянной a².

Если отрезок АВ лежит на прямой l , a CD - на прямой m, то искомое геометрическое место состоит из четырех отрезков, образующих параллелограмм PQRS, в котором l и m -диагонали, а положение вершин Р и Q определяется из соотношений

h_PCD = a², h_Q AB = a², (1)

где h_P и h_Q - расстояния точек Р и Q от прямых m и l.

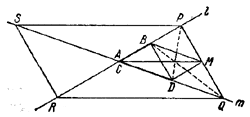
Доказательство. Заметим, что при фиксированных l и m искомое геометрическое место вполне определяется заданием длин отрезков АВ и CD и постоянной a, но не зависит от положения этих отрезков на прямых l и m. Действительно, при изменении этого положения площади треугольников АМВ и CMD не меняются. Поэтому достаточно рaссмотреть частный случай, когда отрезки АВ и CD имеют общий конец в точке пересечения прямых l и m. В этом случае отрезки АВ и CD будут сторонами треугольника, третья сторона которого лежит в одном из четырех углов, образующихся при пересечении прямых l и m. Например, на рис. 127 совмещены концы А и С и третьей стороной является BD.

Пусть М-точка искомого геометрического места, лежащая внутри угла BAD. Тогда площадь \(\Delta\)BMD равна

S_BMD = | S_AMB + S_CMD - S_ABD | = | a² - S_ABD |

Отсюда следует, что расстояние точки М от прямой BD не зависит от ее положения на прямой PQ || BD. Для точек Р || Q выполнены соотношения (1).

Обратно, пусть М - какая-нибудь точка на прямой PQ, где точки Р и Q построены согласно (1). Из соотношений

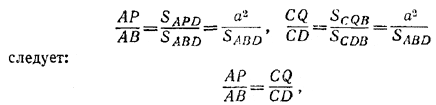
т. е. PQ || BD. Поэтому

S_AMB + S_CMD = S_ABD+ S_BMD = S_ABD+ S_BPD = S_APD = a²

Следовательно, точка М принадлежит искомому геометрическому месту. Остальные стороны параллелограмма PQRS получаются аналогично при совмещении других концов отрезков, а именно: QR при В = С, RS при В = D и SP при A = D.