Найти геометрическое место точек, для которых разность расстояний до двух данных прямых m и l равна отрезку данной длины. Разобрать случаи параллельных и пересекающихся прямых.

В случае пересекающихся прямых искомое геометрическое место состоит из восьми полупрямых, являющихся продолжениями сторон прямоугольника ABCD, указанного в решении задачи 323.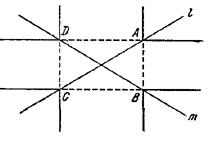

Доказательство аналогично тому, которое дано в решении этой задачи.

Если данные прямые l и m параллельны и расстояние между ними равно h, то искомое геометрическое место существует только тогда, когда a < h, и представляет собой пару прямых, параллельных данным, при а < h или часть плоскости, лежащую вне полосы между l и m, при a = h.