Даны две параллельные прямые и точка О, лежащая между ними. Через эту точку проводят произвольную секущую, которая пересекает параллельные прямые в точках А и А'. Найти геометрическое место концов перпендикуляра к секущей, восставленного из точки А' и имеющего длину OA.

Искомое геометрическое место состоит из двух прямых l и k, симметрично расположенных относительно общего перпендикуляра ВВ' к данным параллельным прямым, проведенного через точку О. Прямая l проходит через точку С перпендикулярно к ОС, причем В'С = ОВ.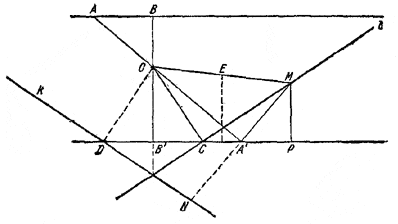

Доказательство. Пусть М и N - точки, полученные при построении с помощью секущей А А'. Доказательство проведем только для точки М (для N оно проводится аналогично).

Пусть MР⊥В'С; тогда ∠ОАВ = ∠А'МР (как углы с перпендикулярными сторонами). Поэтому прямоугольные треугольники ОАВ и А'МР, имеющие равные гипотенузы ОА и А'М, равны. Значит, А'Р = ОВ = В'С. Отсюда следует, что если Е - середина ОМ, то точки М, А', С, О лежат на одной окружности с центром E и, следовательно, МС⊥ ОС, т. е. точка М лежит на прямой l . Обратно, если М-какая-нибудь точка прямой l и ∠МА'О прямой, то А'Р = В'С = ОВ, откуда следует равенство треугольников ОАВ и А'МР и, наконец, равенство ОА = А'М. Следовательно, точка М получается рассматриваемым построением.