В равнобедренном треугольнике с основанием, равным 4 см, и высотой, равной 6 см, на боковой стороне, как на диаметре, построена полуокружность. Точки пересечения ее с основанием и боковой стороной соединены прямой. Определить площадь получившегося четырехугольника, вписанного в полукруг.

Площадь S четырехугольника ADEB равна

S = S_АВС - S_DEC

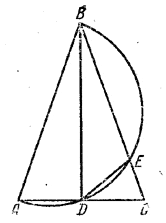
Имеем

Для разыскания S_DEC заметим, что треугольники DEС и DBC имеют общую вершину D и одну и ту же высоту (на чертеже не обозначенную), причем

S_DBC = ¹/₂ S_АВС = 6 см².

Следовательно,

S_DEC : 6 = СE : СВ.

Неизвестный отрезок СЕ найдем из свойства секущих, проведенных из одной точки (С). Имеем CE • CB = CD • CA,

откуда . Следовательно,

Отв. S = 10,8 см².