Шар вписан в прямую призму, в основании которой лежит прямоугольный треугольник. В этом треугольнике перпендикуляр длины h, опущенный из вершины прямого угла на гипотенузу, составляет с одним из катетов угол α. Найти объем призмы.

Пусть R - радиус шара и пусть а, b и с - соответственно катеты и гипотенуза треугольника ABC, лежащего в основании.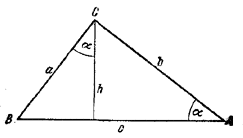

Имеем:

Очевидно, радиус R равен радиусу круга, вписанного в \(\Delta\)ABC, Поэтому

и, следовательно, объем призмы равен