Рассматривается проекция куба с ребром а на плоскость, перпендикулярную к одной из диагоналей куба. Во сколько раз площадь проекции будет больше площади сечения куба плоскостью, проходящей через середину диагонали куба перпендикулярно к ней?

В проекции получится правильный шестиугольник со стороной, равной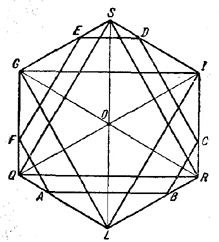 Чтобы в это убедиться, удобно представить себе результат проектирования всевозможных сечений куба, рассмотренных в задаче 225. Все указанные сечения проектируются без изменения размеров, и мы получим фигуру, показанную на рис.

Пользуясь тем, что сторона треугольника RQS равна а√2 , из треугольника GOS находим:

откуда 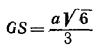. Tак как далее сторона правильного шестиугольника A₁B₁C₁D₁E₁F₁(см. рис.) равна , то искомое отношение площадей оказывается равным