От правильной четырехугольной призмы плоскостью, проходящей через диагональ нижнего основания и одну из вершин верхнего основания, отсечена пирамида с полной поверхностью S. Найти полную поверхность призмы, зная, что угол при вершине треугольника, получающегося в сечении, равен а.
Пусть а - длина стороны квадрата, лежащего в основании призмы, l - длина бокового ребра призмы, d - диагональ боковой грани.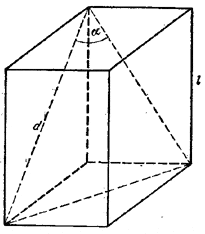
Обозначим через Sсеч. площадь сечения; легко видеть, что полная поверхность призмы равна 4 (S - Sсеч.); поэтому достаточно определить Sсеч.. Имеем:
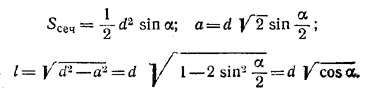
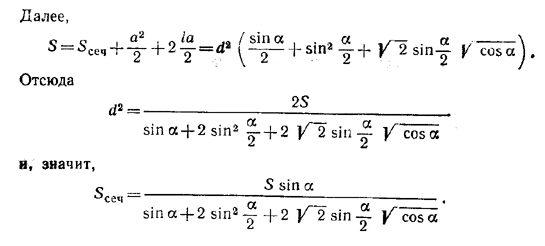
В итоге после упрощений находим, что полная поверхность призмы равна
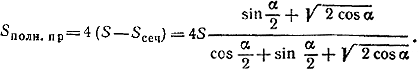
Похожие примеры: