Найти поверхность правильной n-угольной пирамиды объема V, если радиус круга, вписанного в основание, равен радиусу круга, описанного вокруг сечения, параллельного основанию и отстоящего от основания на расстоянии h.
Пусть Н - высота пирамиды, х - высота боковой грани, проведенная из вершины пирамиды, R - радиус круга, вписанного в основание, r - радиус круга, описанного около основания, а - сторона основания.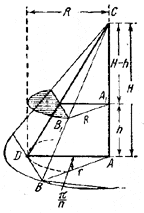
Из подобия треугольников СА1В1 и CAB получаем:
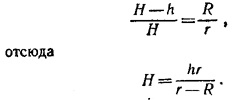
Но из \(\Delta\)ADB имеем 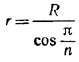 , и поэтому
, и поэтому 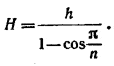
Так как, далее, для площади основания и объема имеем следующие формулы:
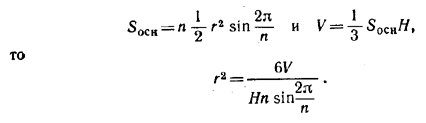
Подставляя сюда найденное выражение для H, находим:
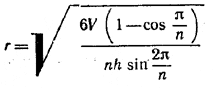
Так как, далее, х = √ R2+ H2 и a/2 = rsin π/n, то боковая поверхность равна
n 1/2 xa = nr sin π/n√ R2+ H2
или окончательно
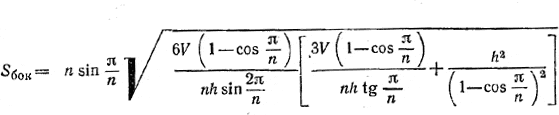
Похожие примеры: