Окружность разделена произвольным образом на четыре части, и середины получающихся дуг соединены отрезками прямых. Показать, что среди этих отрезков два будут перпендикулярны между собой.

Пусть В₁ , В₂, В₃, В₄ — середины дуг А₁А₂, А₂А₃, A₃A₄, A₄A₁.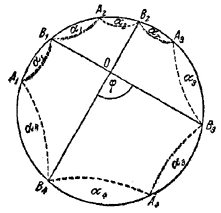

Пусть α_i — центральный угол, соответствующий дуге A_i B_i (i = 1, 2, 3, 4). Обозначим через φ угол, образованный отрезками В₁В₃ и В₂В₄. Тогда

а так как

2α₁ + 2α₂ + 2α₃ + 2α₄ = 2π,

то φ = ^π/₂