Доказать, что прямая, соединяющая середины параллельных сторон трапеции, пройдет через точку пересечения диагоналей.

Пусть дана трапеция ABCD с параллельными основаниями AD и ВС, E — середина ВС, F — середина AD и О — точка пересечения диагоналей.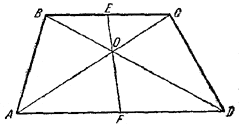

Треугольники AOF и СОЕ подобны (это следует из подобия треугольников AOD и СОВ). Поэтому ∠AOF = ∠СОЕ, т. е. EOF — прямая.