Доказать, что сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон с удвоенным произведением оснований.

Пусть ABCD — данная трапеция с основаниями AD и ВС и пусть BE ⊥ AD, CF ⊥ AD.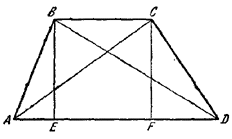

Имеем:

AC² — AF² = CD² — FD²,

BD² — ED² = AB² — AE².

Сложив эти равенства, получим:

АС² + BD² = AВ² + CD² + AF² — FD² + ED² — AE² =

= AВ² + СD² + AD(AF — FD + ED — AE)=

= AВ² + CD² + AD • 2EF = AВ² + CD² + 2AD • ВС.