В треугольнике из основания каждой высоты опущены перпендикуляры на две другие стороны. Доказать, что: 1) основания этих перпендикуляров являются вершинами шестиугольника, три из сторон которого параллельны сторонам треугольника; 2) вокруг этого шестиугольника можно описать окружность.

В \(\Delta\)АВС пусть АА₁, ВВ₁ , СС₁ — высоты, пересекающиеся в точке О,
C₁M || B₁N ⊥BC, A₁P || C₁Q ⊥ AC, В₁R || A₁S⊥ АВ.

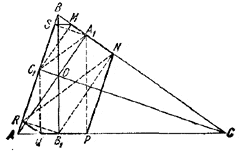
1) Докажем, что SM || АС. Имеем \(\Delta\) ВА₁А ~ \(\Delta\)BC₁C как прямоугольные треугольники с общим острым углом ABC. Поэтому

Следовательно, \(\Delta\)А₁BC₁ ~ \(\Delta\) ABC и ∠ВА₁С₁ = ∠ВАС. В \(\Delta\)А₁ВС₁ отрезки A₁S и С₁М — высоты. Поэтому, повторив предыдущее рассуждение, покажем, что ∠BSM = ∠BA₁C₁. Следовательно, ∠BSM = ∠ВАС и SM || AС. Аналогично доказывается, что PN || АВ и RQ || BC.

2) Для доказательства того, что вершины шестиугольника MNPQRS лежат на одной окружности, достаточно доказать, что любые четыре его последовательные вершины лежат на одной окружности. Это следует из того, что через три точки, не лежащие на одной прямой, можно провести только одну окружность. Имеются четверки последовательных вершин рассматриваемого шестиугольника двух типов: такие, в которых средние точки лежат на разных сторонах \(\Delta\)ABC (RSMN, MNPQ, PQRS), и такие, в которых средние точки лежат на одной стороне \(\Delta\)ABC (NPQR, QRSM, SMNP).

Рассмотрим четверки RSMN и NPQR (разных типов). Из очевидной пропорциональности

следует, что NR || A₁C₁ Поэтому

∠MNR = ∠BA₁C₁ = ∠ВАС = ∠BSM.

Значит, ∠MNR + ∠MSR = π и точки R, S, М, N лежат на одной окружности. Далее,

∠PNR + ∠PQR = π — (∠PNC + ∠BNR) + π — ∠AQR =
= 2π — (∠ABC+ ∠ВАС + ∠AСВ) = π,

откуда следует, что точки N, P, Q, R также лежат на одной окружности. Аналогично проводится доказательство для остальных четверок.