Доказать, что середины сторон треугольника, основания высот и середины отрезков высот, заключенных между каждой из вершин и точкой пересечения высот, представляют собой девять точек, лежащих на одной окружности. Показать, что центр этой окружности лежит на середине отрезка, соединяющего точку пересечения высот данного треугольника с центром описанного круга, а радиус равен половине радиуса описанного круга.

Пусть в \(\Delta\) ABC точка М есть точка пересечения высот АА₁, ВВ₁ , СС₁; Р — центр описанного круга радиуса R; С₂, А₂, В₂ — середины сторон АВ, ВС, AC; ОМ = ОР; ON ⊥ AC; A₃, В₃, С₃ — середины AM, ВМ, СМ.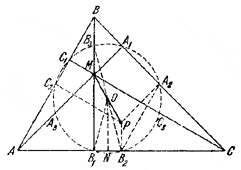

Докажем, что точка О находится на равном расстоянии от А_i , В_i , С_i , где i= 1, 2, 3. Так как ON — средняя линия в трапеции МВ₁В₂Р, то OB₁ = OB₂. Из подобия треугольников АМВ и РА₂В₂ находим ВМ = 2РВ₂, поэтому B₃M = PB₂. Из параллелограмма МВ₃РВ₂ имеем ОВ₃ = ОВ₂. Но

ОВ₃ = ¹/₂ BP = ^R/₂

(как средняя линия в треугольнике РМВ). Следовательно,

ОВ₂= ОВ₂= ОВ₁ = ^R/₂.

Точно так же доказывается, что ОА₁ = ОА₂ = OА₃ = ОС₁ = ОC₂= ОC₃= ^R/₂