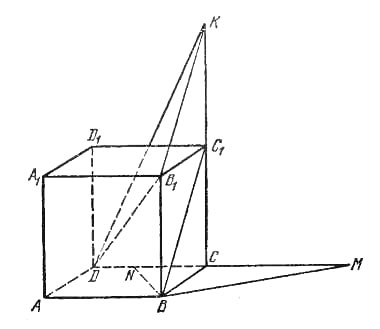
Дан куб ABCDA1B1C1D1; через ребро АА1 проведена плоскость, образующая равные углы с прямыми BC и B1D. Найти эти углы.
Возьмем на продолжении ребра СС1 точку К так, что В1К || ВС1, а через ребро ВВ1 проведем плоскость, параллельную данной (рис.). Эта плоскость должна проходить или через внутреннюю, или через внешнюю биссектрису угла DB1K. Поскольку отношение, в котором плоскость, проходящая через ВВ1, делит DК1, равно отношению, в котором она делит DC, возможны два случая: плоскость проходит через точку N на ребре DC такую, что \(\frac{|DN|}{|NC|}=\frac{\sqrt3}{\sqrt2}\), или же она проходит через тешу М на его продолжении и опять \(\frac{|DM|}{|MC|}=\frac{\sqrt3}{\sqrt2}\).
Найдем расстояние от точки К до первой плоскости. Оно равно расстоянию от точки С до прямой BN. Если это расстояние x, то
$$ x=\frac{2S_{BNC}}{|BN|}=\frac{a\sqrt2}{(\sqrt3+\sqrt2)\sqrt{11-4\sqrt6}}=\frac{a(\sqrt6 -1)\sqrt2}{5} \\ \text{и} \\ sin\phi = \frac{x}{|B_1K|}=\frac{\sqrt6 -1}{5} $$где \(\phi\) - угол между плоскостью ВВ1N и прямыми B1D и В1К.
Точно так же находится другой угол.
Ответ: \(arcsin\frac{\sqrt6\pm 1}{5}\)