Через данную точку А провести плоскость, параллельную данной плоскости (Р), не проходящей через точку А
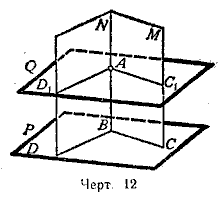
Проводим на плоскости Р через какую-либо точку В две какие-либо прямые ВС и ВD. Построим две вспомогательные плоскости: плоскость М-через точку А и прямую ВС и плоскость N - через точку А и прямую ВD. Искомая плоскость, параллельная плоскости Р, должна пересечь плоскость М по прямой, параллельной BС, a плоскость N - по прямой, параллельной ВD.
Отсюда вытекает такое построение:
через точку А проводим в плоскости М прямую АС1 || ВС, а в плоскости N прямую АD1 || ВD.
Через прямые АС1 и АD1 проводим плоскость Q. Она и будет искомой. В самом деле, стороны угла D1АС1 расположенного в плоскости Q параллельны сторонам угла DВС, расположенного в плоскости P. Следовательно, Q || Р.
Так как в плоскости М через точку А можно провести лишь одну прямую, параллельную ВС, а в плоскости N через точку А лишь одну прямую, параллельную BD, то задача имеет единственное решение. Следовательно, через каждую точку пространства можно провести единственную плоскость, параллельную данной плоскости.