В основание конуса вписан квадрат, сторона которого равна а. Плоскость, проходящая через вершину конуса и сторону квадрата, дает в сечении с поверхностью конуса треугольник, угол при вершине которого α. Определить объем и полную поверхность конуса.

Радиус основания конуса R = a/√2 (рис.).

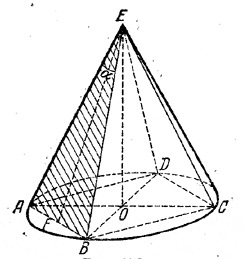
Из \(\Delta\)АЕF находим 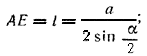из \(\Delta\)АОE находим

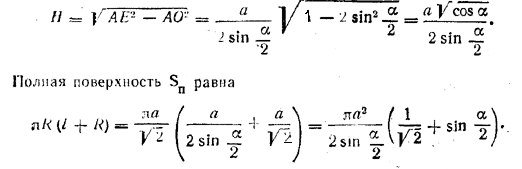
Выражение в скобках можно преобразовать следующим образом:





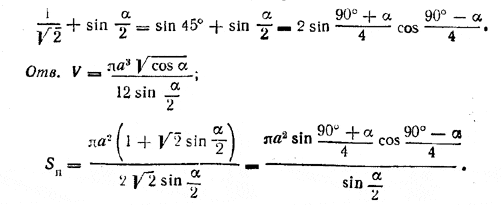
Похожие примеры:
Вычислить радиусы оснований усеченного конуса, описанного около шара радиуса R, зная, что отношение полной поверхности усеченного конуса к поверхности шара равно т. Смотреть решение→
На плоскости Р лежат три равных шара радиуса R, касающиеся друг друга. Прямой круговой конус расположен так, что его плоскость основания совпадает с Р, а данные шары касаются конуса и лежат вне его. Найти радиус основания конуса, если его высота задана и равна qR.  Смотреть решение→
Радиус основания конуса равен R, а угол при вершине осевого сечения равен α. Найти объем правильной треугольной пирамиды, описанной вокруг конуса. Смотреть решение→