Ромб

Построим угол и на его сторонах отложим от вершины А равные отрезки АВ = АС (рис. 239).

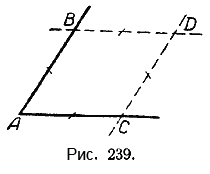
Через точку В проведём прямую, параллельную АС; через точку С проведём прямую, параллельную АВ. Точку пересечения этих прямых обозначим через D. Мы получили параллелограмм АВDС, причём ВD = АС, СD = АВ, как противоположные стороны параллелограмма. Отсюда: ВD = АС = АВ = DС.

Параллелограмм, у которого все стороны равны, называется ромбом.

Свойства ромба.

Так как ромб есть параллелограмм, то он обладает всеми его свойствами.

1. Диагональ ромба делит его на два равных треугольника.

2. Диагонали ромба в точке их пересечения делятся пополам.

3. Противоположные стороны ромба равны между собой, равны и противоположные углы его.

Кроме того, ромб обладает ещё следующими свойствами:

а) диагонали ромба взаимно перпендикулярны;

б) диагональ ромба делит угол его пополам.

В ромбе АВСD проведём две диагонали АС и ВD (рис. 240), пересекающиеся в точке О, и докажем, что АС⊥ ВD, а диагональ АС делит угол С пополам.

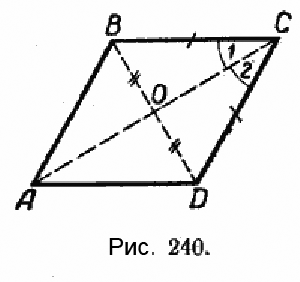
В равнобедренном треугольнике ВСD отрезок СD является медианой, а следовательно, и высотой, и биссектрисой угла С. Отсюда АС ⊥ВD и ∠1 = ∠2. Так же доказывается, что диагональ АС делит пополам угол А, а диагональ ВD делит пополам углы В и D.