Площадь параллелограмма

Пусть требуется найти площадь параллелограмма АВСD (рис. 272, а). Примем сторону АВ за основание параллелограмма и из вершин D и С проведём высоты DМ и СK. Площадь полученного прямоугольника МKСD равна произведению МК на DМ.

Треугольники АDМ и ВСК равны, так как они имеют по равной гипотенузе и по равному катету: АD = ВС и DМ = СK.

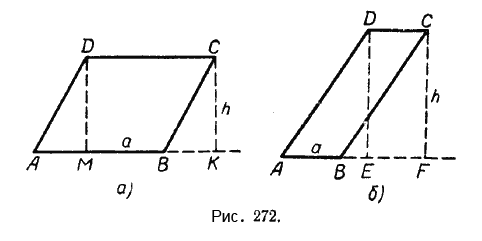
Параллелограмм АDСВ состоит из трапеции МDСВ и треугольника АDМ, прямоугольник МDСК состоит из той же трапеции МDСВ и треугольника ВСК, который равен треугольнику АDМ. Следовательно, площадь параллелограмма равна площади прямоугольника. Отсюда площадь параллелограмма равна также произведению МК на DМ. Но МК = АВ (МК = DС = АВ), поэтому площадь параллелограмма будет равна произведению АВ на DМ, т. е.

площадь параллелограмма равняется произведению его основания на высоту.

S_{параллелограмма} = а • h, где а - основание параллелограмма и h - его высота.

Несколько иное рассуждение придётся применить для вывода формулы площади параллелограмма, изображённого на чертеже 272, б, где АВСD - данный параллелограмм, а ЕFСD - вспомогательный прямоугольник.

S_ABCD =S_AFCD - S_BCF,

S_EFCD = S_AFCD - S_ADE, но

\(\Delta\)ВСF = \(\Delta\)АDЕ, следовательно,

S_ABCD = S_EFCD = СD • СF, т. е.

S_ABCD = а • h.