Признаки параллелограмма
Теорема 1. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
Пусть в четырёхугольнике AВDС (рис. 227) АВ = СD и АС = ВD. Докажем, что при этом условии АВ || СD и АС || ВD, т. е. четырёхугольник АВDC — параллелограмм.
Соединим отрезком какие-нибудь две противоположные вершины этого четырёхугольника, например С и В. Четырёхугольник ABDС разбился на два равных треугольника: \(\Delta\)СAВ и \(\Delta\)СDВ. В самом деле, сторона СВ у них общая, AB = СD и АС = ВD по условию. Таким образом, три стороны одного треугольника соответственно равны трём сторонам другого, поэтому \(\Delta\)СAВ = \(\Delta\)СDВ.
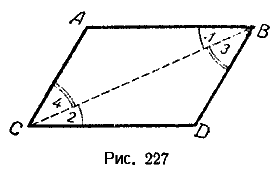
В равных треугольниках против равных сторон лежат равные углы, поэтому
∠1 = ∠2 и ∠3 = ∠4.
Углы 1-й и 2-й являются внутренними накрест лежащими углами при пересечении прямых AB и СD прямой СВ. Следовательно, AB || СD.
Точно так же углы 3-й и 4-й являются внутренними накрест лежащими углами при пересечении прямых CA и ВD прямой СВ, следовательно, CA || ВD.
Таким образом, противоположные стороны четырёхугольника ABDС попарно параллельны, следовательно, он - параллелограмм, что и требовалось доказать.
Теорема 2. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
Пусть в четырёхугольнике ABDС AB = СD и AB || СD. Докажем, что при этих условиях четырёхугольник ABDС — параллелограмм (рис. 228).
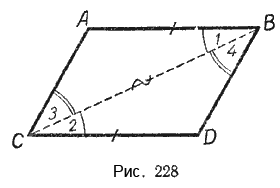
Соединим отрезком СВ вершины С и В. Вследствие параллельности прямых AB и СD углы 1 и 2, как углы внутренние накрест лежащие, равны.
Тогда треугольник СAB равен треугольнику СDВ, так как сторона СВ у них общая,
AB = СD по условию теоремы и ∠1 = ∠2 по доказанному.
Из равенства этих треугольников вытекает равенство углов 3 и 4, так как они лежат против равных сторон в равных треугольниках.
Но углы 3 и 4 — это внутренние накрест лежащие углы, образованные при пересечении прямых АС и ВD прямой СВ, следовательно, АС || ВD, т. е. четырёхугольник ABDС — параллелограмм.
Теорема 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.
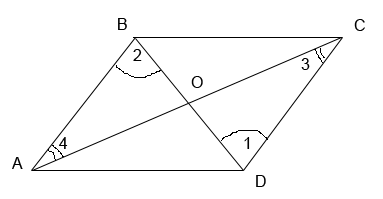
Треугольники \(\Delta\)AOB и \(\Delta\)COD будут равны между собой по первому признаку равенства треугольников (AO = OC, BO = OD по условию, ∠AOB = ∠COD - как вертикальные углы.)
Следовательно, AB = CD и ∠1 = ∠2. Из равенства углов 1 и 2 имеем, что AB || CD.
Тогда имеем, что в четырехугольнике ABCD стороны AB = CD и AB || CD, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
Признаки параллелограмма кратко:
1. Противоположные стороны попарно равны
2. Противоположные стороны равны и параллельны
3. Диагонали пересекаются и в точке пересечения делятся пополам