Квадрат

Построим прямой угол и на его сторонах отложим равные отрезки АВ и АС (рис. 241).

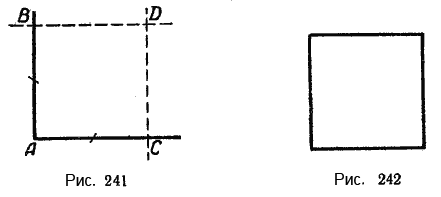
Через точки В и С проведём прямые, параллельные сторонам АС и А В. Точку пересечения их обозначим через О. Мы получили четырёхугольник, в котором:

а) противоположные стороны попарно параллельны, следовательно, это параллелограмм;

б) все углы прямые, следовательно, это прямоугольник;

в) все стороны равны, следовательно, это ромб.

Прямоугольник, в котором все стороны равны, называется квадратом

(рис. 242).

Может быть дано и такое определение квадрата: ромб, у которого все углы прямые, называется квадратом.

Свойства квадрата.

Так как квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает всеми их свойствами.

1. Диагональ квадрата делит его на два равных треугольника.
   
2. Диагонали квадрата в точке их пересечения делятся пополам.
   
3. Противоположные стороны квадрата равны между собой, равны и противоположные углы его. (Свойства параллелограмма.)
   
4. Диагонали квадрата равны. (Свойство прямоугольника.)
   
5. Диагонали квадрата взаимно перпендикулярны.
   
6. Диагональ квадрата делит его угол пополам. (Свойства ромба.)