Подобные многогранники

Определение: Два многогранника называются подобными, если они имеют равные многогранные углы и, соответственно, подобные грани.

Соответственные элементы подобных многогранников называются сходственными.

Из этого определения следует, что в подобных многогранниках:

1. Двугранные углы соответственно равны и одинаково расположены, потому что многогранные углы равны.
2. Сходственные ребра пропорциональны, потому что в каждых двух подобных гранях отношение сходственных ребер одно и то же, и в каждом многограннике соседние грани имеют по общему ребру.

Возможность существования подобных многогранников доказывается следующей теоремой:

Теорема. Если в пирамиде (рис.) проведем секущую плоскость (A₁B₁С₁D₁E₁) параллельно основанию, то отсечем от нее другую пирамиду
(SA₁B₁С₁D₁E₁), подобную данной.

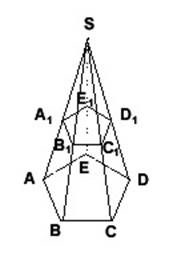
Так как A₁B₁ || AB, B₁С₁ || BC и т.д., то боковые грани двух пирамид подобны.

Основания их также подобны.

Остается доказать равенство многогранных углов.

Угол S у обеих пирамид общий.

Трехгранные углы A₁, B₁, С₁ ... равны соответственно углам A, B, С ..., потому что у каждой пары этих углов плоские углы соответственно равны и одинаково расположены.

Теорема. Две призмы или две пирамиды подобны, если основание и боковая грань одной и основание и боковая грань другой соответственно подобны, одинаково наклонены и одинаково расположены.

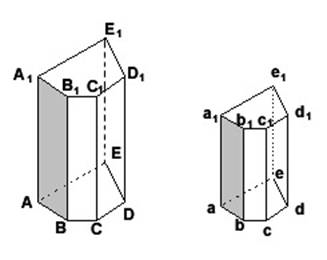
1. Пусть у двух призм (рис.) соответственно подобны и одинаково расположены основания ABCDE, abcde и грани AA₁B₁B, aa₁b₁b и, кроме того, равны двугранные углы AB и ab.

Для доказательства подобия этих призм рассуждаем в такой последовательности:

Трехгранные углы B и b равны, потому что они имеют по равному двугранному углу (AB и ab), заключенному между двумя соответственно равными и одинаково расположенными плоскими углами (ABС=abс и ABB₁=abb₁).

Отсюда следует, что равны плоские углы B₁BC и b₁bс, а также и двугранные BC и bс.

Если же у двух параллелограммов BB₁С₁С и bb₁с₁с имеется по одному равному углу, то и остальные их углы соответственно равны.

Так как, сверх того,

\( \frac{BC}{bc}=\frac{AB}{ab} \) (из подобия оснований) \( \frac{BB_1}{bb_1}=\frac{AB}{ab} \) (из подобия боковых граней)

то

$$ \frac{BC}{bc}=\frac{BB_1}{bb_1} $$

Значит, грани BB₁С₁С и bb₁с₁с подобны.

Переходя теперь к трехгранным углам С и с, совершенно также убедимся, что они равны и что грани СС₁D₁D и сс₁d₁d подобны. Таким образом мы переберем все трехгранные углы при основании и все боковые грани.

Верхние основания A₁B₁С₁D₁E₁ и a₁b₁с₁d₁e₁ подобны, потому что они равны нижним основаниям.

Трехгранные углы при верхних основаниях соответственно равны, потому что у них равны и одинаково расположены плоские углы.

Значит, рассматриваемые призмы подобны.

2. Пусть мы имеем (рис.) две пирамиды, у которых соответственно подобны и одинаково расположены основания ABCDE, abcde и боковые грани SAB, sab и, кроме того, равны двугранные углы AB и ab.

Совершенно так, как это было сделано для призм, мы докажем, что все трехгранные углы, прилежащие к основаниям, соответственно равны, и что все боковые грани соответственно подобны.

Тогда многогранные углы S и s также будут равны, потому что имея все плоские и двугранные углы соответственно равные и одинаково расположенные, они при вложении одного в другой совмещаются.

Теорема. Подобные многогранники могут быть разложены на одинаковое число соответственно подобных и одинаково расположенных пирамид (рис.).

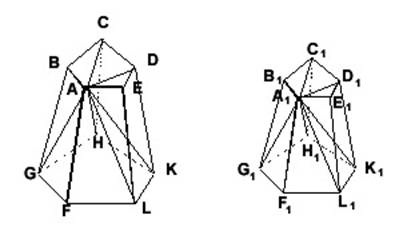
Указанное в теореме разложение может быть выполнено различными способами. Мы поступим так:

Возьмем в одном из данных подобных многогранников вершину A какого-нибудь многогранного угла.

Возьмем далее все те грани многогранника, которые не принадлежат к углу A.

В нашем многограннике таких граней четыре: EDLK, DCHK, СBGH и FGHKL.

Каждую из этих граней примем за основание такой пирамиды, вершина которой лежала бы в A. Тогда многогранник разобъется на пирамиды, сходящиеся вершинами в точке A.

В другом многограннике возьмем сходственную вершину A₁ и тем же путем разложим его на одинаковое число пирамид.

Докажем, что эти пирамиды соответственно подобны.

И действительно, какую бы пару соответственных пирамид мы ни взяли, легко найдем, что основание и грань одной пирамиды и основание и грань другой пирамиды соответственно подобны, одинаково наклонены и одинаково расположены.

Например, у пирамид ADELK, A₁D₁E₁L₁K₁ основания DELK, D₁E₁L₁K₁ подобны, как сходственные стороны подобных многогранников, грани ADE и A₁D₁E₁ подобны, потому что подобные многоугольники ABCDE, A₁B₁С₁D₁E₁ разбиваются на соответственно подобные тр-ки. Двугранные углы DE, D₁E₁ равны, как сходственные углы подобных многогранников.

Из этого следует, что взятые нами пирамиды подобны. То же самое можно сказать о других пирамидах.

Теорема. Поверхности подобных многогранников относятся, как квадраты сходственных ребер.

Пусть P₁, P₂, P₁3 … P_n означают площади отдельных граней одного из подобных многогранников, p₁, p₂, p₃ … p_n площади сходственных граней другого.

Предположим еще, что L и l будут длины двух каких-нибудь сходственных ребер.

Тогда, вследствие подобия сходственных граней и пропорциональности всех сходственных ребер, будем иметь:

$$ \frac{P_1}{p_1}=\frac{L^2}{l^2}; \frac{P_2}{p_2}=\frac{L^2}{l^2}; \frac{P_3}{p_3}=\frac{L^2}{l^2} … \frac{P_n}{p_n}=\frac{L^2}{l^2}; $$
Откуда
$$ \frac{P_1+P_2+P_3...+P_n}{p_1+p_2+p_3...+p_n}=\frac{L^2}{l^2}; $$

Теорема. Объемы подобных многогранников относятся как кубы сходственных ребер.

1. Сначала докажем теорему для подобных пирамид.

Пусть (рис.) пирамиды SABCDE и S₁A₁B₁С₁D₁E₁ подобны.

Вложим вторую пирамиду в первую так, чтобы у них совпали равные многогранные углы S и S₁.

Тогда основание A₁B₁С₁D₁E₁ займет некоторое положение abcde, причем стороны ab, bc, ... соответственно параллельны сторонам AB, BC, ... (вследствие равенства плоских углов трехгранных A и A₁, B и B₁ и т.д.)

Вследствие этого плоскость abcde параллельна ABCDE.

Пусть SO и So высоты двух пирамид.

Тогда:
$$ V_SABCDE = S_ABCDE\cdot\frac{1}{3}SO \\ V_Sabcde = S_abcde\cdot\frac{1}{3}So $$
Следовательно:
$$ \frac{V_SABCDE}{V_Sabcde} = \frac{S_ABCDE}{S_abcde} \cdot \frac{SO}{So} $$
но
$$ \frac{S_ABCDE}{S_abcde} = \frac{{SO}^2}{{So}^2} $$
Поэтому:
$$ \frac{V_SABCDE}{V_Sabcde} = \frac{{SO}^3}{{So}^3} = \frac{{SA}^3}{{Sa}^3} = ... $$

2. Теперь докажем теорему для двух каких угодно подобных многогранников, объемы которых назовем V и v.

Разобьем их на подобные пирамиды.

Пусть V₁, V₂, V₃, … V_n и v₁, v₂, v₃, … v_n будут объемы сходственных пирамид, L и l длины каких-нибудь сходственных ребер. Тогда, согласно доказанному будем иметь:

$$ \frac{V_1}{v_1}=\frac{L^3}{l^3}; \frac{V_2}{v_2}=\frac{L^3}{l^3}; \frac{V_3}{v_3}=\frac{L^3}{l^3}; ... \frac{V_n}{v_n}=\frac{L^3}{l^3}; $$
Откуда
$$ \frac{V_1+V_2+V_3+...+V_n}{v_1+v_2+v_3+...+v_n}=\frac{L^3}{l^3}; $$
Таким образом
$$ \frac{V}{v}=\frac{L^3}{l^3}; $$