Площадь поверхности вращения

Площадь боковой поверхности для цилиндра и конуса можно определить с помощью площади развертки. Однако не для любой поверхности такой способ пригоден. Например, нельзя «развернуть» на плоскость сферу.

Определим в общем случае площадь поверхности вращения и приведем формулу для ее вычисления.

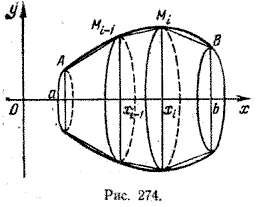
Пусть дана дуга АВ кривой (рис. 274), уравнение которой у = f(х), х \( \in \) [а; b],

где f(х) - неотрицательная функция, имеющая непрерывную производную.

Разобьем отрезок [а; b] точками

$$ x_i = a+\frac{b-a}{n}i, \;\; i=1, 2, ..., n-1, $$

на n отрезков равной длины. Через точки x_i проведем прямые, параллельные оси Оу, точки пересечения этих прямых с дугой АВ обозначим M_i.

Ломаная АМ₁М₂ ... M_n-1B называется вписанной в дугу АВ.

При достаточно мелком разбиении отрезка [а; b], т. е. при достаточно большом n, площади поверхностей, образованных вращением вокруг оси Ох дуги АВ и вписанной в нее ломаной, будут мало отличаться друг от друга.

Поверхность, полученная вращением ломаной, состоит из боковых поверхностей n усеченных конусов (или цилиндров). Ее площадь мы умеем вычислять.

Предел, к которому стремится при п -> ∞ площадь поверхности, образованной вращением ломаной АМ₁ ... M_n-1B, вписанной в АВ, называется площадью поверхности, образованной вращением дуги АВ.

Можно доказать, что площадь поверхности, образованной вращением кривой АВ вокруг оси Ох, вычисляется по формуле

$$ S=2\pi\int_{a}^{b}f(x)\sqrt{1+(f’(x))^2}dx $$

или, короче,

$$ S=2\pi\int_{a}^{b}y\sqrt{1+(y’)^2}dx $$

Доказательство этой формулы мы не приводим.

Задача 1. Найти площадь поверхности, полученной вращением вокруг оси Ох дуги параболы у = 2√x 0 < x < 1 (рис. 275).

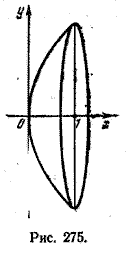
Так как у’ = ¹/_√x , то, согласно формуле (1), площадь поверхности вращения будет выражаться формулой

$$ S=2\pi\int_{0}^{1}2\sqrt{x} \sqrt{1+\frac{1}{x}}dx = 4\pi\int_{0}^{1}\sqrt{1+x}dx $$

откуда получаем

$$ S=\left. 4\pi\cdot \frac{2}{3}(1+x)^{\frac{3}{2}}\right|_0^1 =\\= \frac{8\pi}{3}(2^{\frac{3}{2}}-1) $$

Ответ: S = ^8π/₃ ( 2√2 - 1) .

Если кривая АВ задана параметрическими уравнениями x = φ(t), y = ψ(t), t \( \in \) [α ;β], где φ(t) и ψ(t) имеют непрерывные производные, то

$$ S=2\pi\int_{\alpha}^{\beta}|\psi(t)|\sqrt{(\phi’(t))^2 + (\psi’(t))^2}dt $$

или короче:

$$ S=2\pi\int_{\alpha}^{\beta}|y|\sqrt{x’^2 + y’^2}dt $$

Задача 2. Вычислить площадь поверхности, образованной вращением вокруг оси Ох дуги циклоиды

$$ \begin{cases} x = a(t-sin t)\\ y = a(1-cos t)\end{cases} \;\; t\in[0;2\pi] $$

Так как х’ = а (1 - cos t) и y’ = а sin t, то по формуле (2) получаем

$$ S=2\pi\int_{0}^{2\pi}a(1-cost)\sqrt{a^2(1-cost)^2 + a^2sin^2t}dt =\\= 2\pi a^2\int_{0}^{2\pi}(1-cost)\sqrt{2(1-cost)}dt =\\= 8\pi a^2\int_{0}^{2\pi} sin^3\frac{t}{2}dt = 8\pi a^2\int_{0}^{2\pi}(1-cos^2\frac{t}{2})sin\frac{t}{2}dt $$

Сделаем замену: \( u=cos\frac{t}{2}, \; du=-\frac{1}{2}sin\frac{t}{2}dt. \) Тогда

$$ S=16\pi a^2\int_{-1}^{1}(1-u^2)du = \frac{64}{3}\pi a^2 $$

Ответ: \( S=\frac{64}{3}\pi a^2 \)