Площадь шара

Теорема 1. Площадь сферы радиуса R вычисляется по формуле

S = 4πR² (1)

Сфера радиуса R может быть получена вращением вокруг оси Ох полуокружности, заданной уравнением

$$ y=\sqrt{R^2 - x^2}, \;\; x \in [- R; R] $$

Тогда по формуле для площади поверхности вращения получаем

$$ S=2\pi\int_{-R}^{R}y\sqrt{1+y’^{2}}dx =\\= S=2\pi\int_{-R}^{R}\sqrt{R^2 - x^2}\sqrt{1+\frac{x^2}{R^2 - x^2}}dx =\\= S=2\pi\int_{-R}^{R}Rdx = 4\pi R^2 $$

Аналогично выводится формула для площади сферического пояса, который получается вращением вокруг оси Ох дуги окружности (рис. 276) \( y=\sqrt{R^2 - x^2}, \;\; x \in [a; b]\)

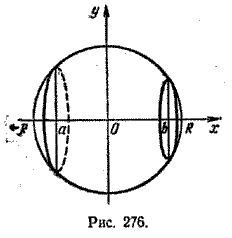
Действительно,

$$ S=2\pi\int_{a}^{b}y\sqrt{1+y’^{2}}dx = 2\pi\int_{a}^{b}Rdx = 2\pi R(b-a) \;\; (2) $$

Теорема 2. Площадь сферического пояса радиуса R и высоты Н вычисляется по формуле

S = 2πRH. (3)

Формула (3) получается из формулы (2), так как Н = b - а.

Сферический сегмент можно получить вращением дуги окружности

$$ y=\sqrt{R^2 - x^2}, \;\; a \leq x \leq R $$

вокруг оси Ох. Следовательно, сферический сегмент есть частный случай сферического пояса (b = R).

Следствие. Площадь сферического сегмента радиуса R и высоты Н вычисляется по формуле (3).

3 а д а ч а. В сферу вписан куб с ребром а (рис. 277).

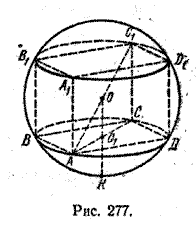
Найти площади:

а) сферы;

б) сферического пояса, отсекаемого плоскостями верхней и нижней граней куба;

а) Диагональ куба с ребром а равна √3 а. Следовательно, |АС₁| = √3 а. С другой стороны, если R - радиус сферы, то | АС₁| = 2R. Поэтому 2R = √3 а, т. е. R= ^√3/₂ a.

По формуле (1) находим площадь S сферы: S = 4πR² = 4π ³/₄ а² = 3π а² .

б) Высота сферического пояса в данном случае, очевидно, равна а. Положив в формуле (3) Н = а и R = ^√3/₂ a, найдем площадь S₁ сферического пояса

S₁ = 2πRH = 2π ^√3/₂ а² = π√3 а² .

в) Высота сферического сегмента равна длине отрезка O₁K. Вычислим ее:

|О₁К| = |OK| - |OO₁| = R- ^a/₂ = ^√3/₂ a - ^a/₂ = ^√3-1/₂ a

Положив в формуле (3) Н = ^√3-1/₂ a и R= ^√3/₂ a, найдем площадь S₂ сферического сегмента:

S₂ = 2πRH = 2π ^√3/₂ а ^√3-1/₂ a = π ^3-√3/₂ a²