Плоскость, касательная к сфере

Определение. Плоскость, имеющая с шаровой поверхностью только одну общую точку, называется касательной плоскостью. Возможность существования такой плоскости доказывается следующей теоремой.

Теорема. Плоскость (Р, черт. 140), перпендикулярная к радиусу (АО) в конце его, лежащем на поверхности шара, есть касательная плоскость.

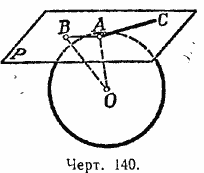
Возьмём на плоскости Р произвольную точку В и проведём прямую ОВ. Так как ОВ - наклонная, а ОА - перпендикуляр к плоскости Р, то ОВ > ОА. Поэтому точка В лежит вне шаровой поверхности; следовательно, у плоскости Р есть только одна общая точка А с шаровой поверхностью; значит, эта плоскость касательная.

Обратная теорема. Касательная плоскость (Р, черт. 140) перпендикулярна к радиусу (ОА), проведённому в точку касания.

Так как, по определению, точка А есть единственная общая точка у плоскости с шаровой поверхностью, то всякая другая точка плоскости лежит вне шаровой поверхности и, следовательно, отстоит от центра на большее расстояние, чем А; таким образом, отрезок ОА есть кратчайшее расстояние точки О от плоскости Р, т. е. ОА есть перпендикуляр к Р.

Прямая, имеющая одну общую точку с шаровой поверхностью, называется касательной к шару. Легко видеть, что существует бесчисленное множество прямых, касающихся шара в данной точке. Действительно, всякая прямая (АС, черт. 140), лежащая в плоскости, касательной к шару в данной точке (А), и проходящая через точку касания (А), есть касательная к шару в этой точке.