Угол между касательной и хордой

Теорема. Угол, образованный касательной и хордой, измеряется половиной дуги, заключённой между его сторонами.

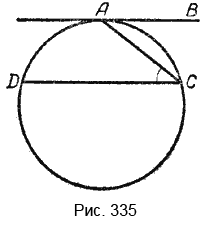
Пусть ∠CAB составлен хордой CA и касательной AB (рис. 335). Требуется доказать, что он измеряется половиной \(\breve{CA}\).
Проведём через точку С прямую СD || AB.
Вписанный ∠АСD измеряется половиной дуги АD, но \(\breve{AD} = \breve{CA}\), так как они заключены между касательной и параллельной ей хордой. Следовательно, ∠DCA измеряется половиной дуги CA.
Так как данный ∠CAB = ∠DCA, то и он измеряется половиной дуги CA.