Площадь круга, сектора

Разделим окружность на возможно большее число равных частей, все полученные точки деления соединим с центром окружности, а соседние - друг с другом хордами.

Таким образом получим ряд равных равнобедренных треугольников (черт. 339).

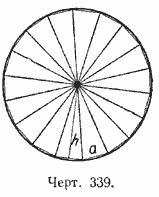
Площадь каждого треугольника равна ^ah/₂, где а - основание его, h - высота.

Обозначив через S’ сумму площадей всех полученных треугольников, получим формулу:

$$ S’=\frac{ah}{2}\cdot n \;\; или \;\; S’=\frac{an \cdot h}{2} $$, где n - число треугольников.

Сумма площадей всех треугольников (S’) весьма близка к площади круга (S), сумма оснований всех треугольников (an) весьма близка к длине окружности (C), а высота (h) каждого треугольника весьма близка к радиусу (r) круга.

Если пренебречь незначительными различиями в размерах, то получим формулу площади круга:

$$ S_{кр} = \frac{Cr}{2} $$

После преобразования получим \( S_{кр} = \frac{2\pi r \cdot r}{2} \), или S_кр = π r²; а обозначив через D диаметр круга, получим:
$$ S_{кр} = \frac{\pi D^2}{4} $$

Примечание. В формуле \(S_{кр} = \frac{Cr}{2}\) поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы его считать приближённым, но в старших классах доказывается, что равенство \(S_{кр} = \frac{Cr}{2}\) не приближённое, а точное.

Другое доказательство:

Впишем в круг, радиус которого обозначим R, какой-нибудь правильный многоугольник.

Пусть площадь этого многоугольника будет q, периметр - р, апофема - а.

По формуле вычисления площади правильного многоугольника имеем:

q = ¹/₂pa.

Вообразим теперь, что число сторон этого многоугольника неограниченно удваивается. Тогда периметр р и апофема а (следовательно, и площадь q) будут увеличиваться, причём периметр будет стремиться к пределу, принимаемому за длину C окружности, апофема будет стремиться к пределу, равному радиусу R круга. Из этого следует, что площадь многоугольника, увеличиваясь при удвоении числа сторон, будет стремиться к пределу, равному ¹/₂С • R. Предел этот принимается за численную величину площади круга. Таким образом, обозначив площадь круга буквой К, можем написать:

K = ¹/₂С • R,

т. е. площадь круга равна половине произведения длины окружности на радиус.

Так как С = 2πR, то

К = ¹/₂• 2πR • R = πR²,

т. е. площадь круга равна квадрату радиуса, умноженному на отношение длины окружности к диаметру.

Следствие. Площади кругов относятся, как квадраты радиусов или диаметров.

Действительно, если K и K₁ будут площади двух кругов, a R и R₁ — их радиусы, то

K = πR² и K₁ = πR₁²,

откуда

$$ \frac{K}{K_1} = \frac{\pi R^2}{\pi {R_1}^2} = \frac{R^2}{{R_1}^2} = \frac{4R^2}{4{R_1}^2} = \frac{(2R)^2}{(2{R_1})^2} $$

Площадь сектора

Сектором называется часть круга, ограниченная двумя радиусами и дугой. На чертеже 340 сектор AOB заштрихован.

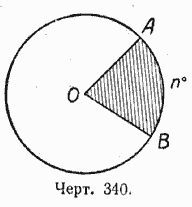
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.

Получаем формулу:
$$ S = \frac{\pi r^2 n}{360} $$ где S - площадь сектора.