Отношение длины окружности к диаметру

Рассматривая процесс нахождения длины окружности, можно заметить, что число, на которое нужно умножить диаметр, чтобы получить длину окружности, не зависит от величины самого диаметра, так что если мы нашли, что длина какой-нибудь окружности равна её диаметру, умноженному на некоторое число, то и длина всякой другой окружности будет равна её диаметру, умноженному на то же самое число.

В самом деле, возьмём две окружности: одну радиуса R, другую радиуса r. Длину первой окружности обозначим через С, длину второй - через c. Впишем в каждую из них правильный многоугольник с одним и тем же числом сторон и будем удваивать число сторон каждого из этих многоугольников.

Обозначим через Р_n переменный периметр правильного многоугольника, вписанного в первую окружность, и через р_n переменный периметр правильного многоугольника с тем же числом сторон, вписанного во вторую окружность.

На основании формулы P_n = 2Rn • sin ^180°/_n, мы можем написать:

$$ \frac{P_n}{2R} = \frac{p_n}{2r} $$

Переменный периметр Р_n имеет пределом длину С первой окружности. Переменный периметр р_n имеет пределом длину c второй окружности. А потому из равенства \(\frac{P_n}{2R} = \frac{p_n}{2r}\) вытекает ^C/_2R = ^c/_2r .

Таким образом, мы можем сказать, что отношение длины окружности к её диаметру есть число постоянное для всех окружностей.

Это постоянное число принято обозначать греческой буквой π. Обозначение это введено, по всей вероятности, в XVII столетии. Буква π (пи) есть начальная буква греческого слова περιφερεια (окружность).

Мы можем, таким образом, для длины С окружности написать такую формулу:

С = 2R • π, или С = 2πR.

Доказано, что число π является числом иррациональным, и, значит, оно не может быть выражено точно никаким рациональным числом. Но его приближённые значения можно находить различными способами с какой угодно точностью. Приняв периметр вписанного 96-угольника за приближённую длину окружности, мы получим для π приближённое значение 3,14 с недостатком и с точностью до 0, 01. Эта точность для практических целей часто бывает достаточна. Для более точных вычислений можно брать

π ≈ 3,14159.

При решении геометрических задач часто встречается число, обратное числу π, т. е. равное дроби ¹/_π. Полезно запомнить несколько цифр этого числа:

¹/_π = 0,3183098 ...

Длина дуги, содержащей n градусов.

Длина окружности есть 2πR, значит, длина дуги в 1° равна ^2πR/₃₆₀ = ^πR/₁₈₀; следовательно, длина s дуги, содержащей n°, выразится так:

s = ^πRn/₁₈₀

Если дуга выражена в минутах (’) или в секундах ("), то длина её определяется соответственно формулами:

s = ^πRn/_180•60 или s = ^πRn/_{180•60 •60},

где n - число минут или секунд.

Задача. Вычислить с точностью до 1 мм радиус такой окружности, дуга которой, содержащая 81°21’ 36", равна 0,452 м.

Обратив 81°21’ 36" в секунды, получим число 292 896. Из уравнения

0, 452 = ^πR•292896/_{180•60 •60}

находим:

R = ^{0,452•180•60•60}/_292896π = ¹/_π = 0,318 (м)

Задача. Определить число градусов дуги, длина которой равна радиусу.

Заменив в формуле, определяющей длину дуги в n°, величину s на R, получим уравнение:

R = ^πRn/₁₈₀, или 1 = ^πn/₁₈₀,

откуда

n° = ^180°/_π = 180° • ¹/_π = 180° • 0,3183098 = 57°295764 = 57°17’ 44",8.

Заметим, что дуга, равная радиусу, называется радианом.

1 угловой радиан это - центральный угол, опирающийся на такую дугу окружности, длина которой равна радиусу этой окружности.

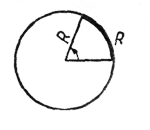
Следовательно:

1(радиан) \(\approx\) 57°17’ 45"

$$ 1° = \frac{2\pi}{360°}\approx 0,017 (радиана) $$

Радианы специального обозначения не имеют. Угол равный α радианов обозначается просто α.

Переход от одного измерения к другому производится по формулам:

$$ \alpha° = \frac{180°}{\pi}\alpha \\ \alpha = \frac{\pi}{180°}\alpha° $$