Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

|CM| = R (1)

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

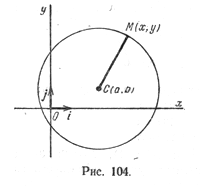
Так как |СМ| = \( \sqrt{(x — a)^2 + (у — b)^2} \), то уравнение (1) можно записать так:

\( \sqrt{(x — a)^2 + (у — b)^2} \) = R

или

(x — a)² + (у — b)² = R² (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

(x — l)² + (y + 3)² = 25

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

x ² + у ² = R². (3)

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

x ² + у ² = 49.

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3)² + (у — (—6))² = 81 или (х — 3)² + (у + 6)² = 81.

Задача 3. Найти центр и радиус окружности

(х + 3)² + (у —5)² =100.

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

x ² + у ² + 4х — 2y — 4 = 0

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

x ² + 4х + 4— 4 + у ² — 2у +1—1—4 = 0

или

(х + 2)² + (у — 1)² = 9.

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

(x +1)² + (y +1)² = ¹⁴⁴/₂₅

Пусть в прямоугольной системе координат дана окружность x ² + у ² = R². Рассмотрим ее произвольную точку М(х; у) (рис. 105).

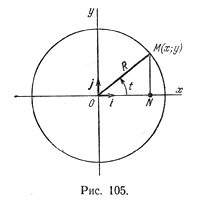
Пусть радиус-вектор OM^> точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0< t < 2?). Выражая х и у через t, находим

x = R cos t ; y = R sin t , 0< t < 2?. (4)

Уравнения (4) называются параметрическими уравнениями окружности с центром в начале координат.

Задача 6. Окружность задана уравнениями

x = \( \sqrt{3}\)cos t, y = \( \sqrt{3}\)sin t, 0< t < 2?.

Записать каноническое уравнение этой окружности.

Из условия следует x ² = 3 cos² t, у ² = 3 sin² t. Складывая эти равенства почленно, получаем

x ² + у ² = 3(cos² t + sin² t )

или x ² + у ² = 3