Свойства вписанных углов
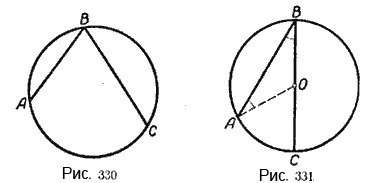
Угол ABC — вписанный угол. Он опирается на дугу АС, заключённую между его сторонами (рис. 330).
Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается.
Это надо понимать так: вписанный угол содержит столько угловых градусов, минут и секунд, сколько дуговых градусов, минут и секунд содержится в половине дуги, на которую он опирается.
При доказательстве этой теоремы надо рассмотреть три случая.
Первый случай. Центр круга лежит на стороне вписанного угла (рис. 331).
Пусть ∠ABC — вписанный угол и центр круга О лежит на стороне BC. Требуется доказать, что он измеряется половиной дуги AC.
Соединим точку A с центром круга. Получим равнобедренный \(\Delta\)AOB, в котором АО = OB, как радиусы одного и того же круга. Следовательно, ∠A = ∠B.
∠AOC является внешним по отношению к треугольнику AOB, поэтому ∠AOC = ∠А + ∠В, а так как углы А и В равны, то ∠В составляет 1/2∠AOC.
Но ∠AOC измеряется дугой АС, следовательно, ∠В измеряется половиной дуги АС.
Например, если \(\breve{AC}\) содержит 60°18’, то ∠В содержит 30°9’.
Второй случай. Центр круга лежит между сторонами вписанного угла (рис. 332).
Пусть ∠ABD — вписанный угол. Центр круга О лежит между его сторонами. Требуется доказать, что ∠ABD измеряется половиной дуги АD.
Для доказательства проведём диаметр BC. Угол ABD разбился на два угла: ∠1 и ∠2.
∠1 измеряется половиной дуги АС, а ∠2 измеряется половиной дуги СD, следовательно, весь ∠АВD измеряется 1/2\(\breve{AC}\) + 1/2\(\breve{CD}\), т. е. половиной дуги АD.
Например, если \(\breve{AD}\) содержит 124°, то ∠В содержит 62°.
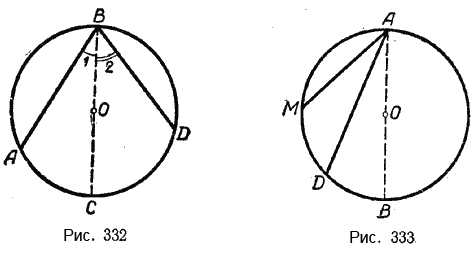
Третий случай. Центр круга лежит вне вписанного угла (рис. 333).
Пусть ∠MAD — вписанный угол. Центр круга О находится вне угла. Требуется доказать, что ∠MAD измеряется половиной дуги MD.
Для доказательства проведём диаметр AB. ∠MAD = ∠MAB — ∠DAB. Но ∠MAB измеряется 1/2\(\breve{MB}\), а ∠DAB измеряется 1/2\(\breve{DB}\).
Следовательно, ∠MAD измеряется 1/2 (\(\breve{MB} — \breve{DB})\), т. е. 1/2\(\breve{MD}\).
Например, если \(\breve{MD}\) содержит 48° 38", то ∠MAD содержит 24° 19’ 8".
Следствия
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги (рис. 334, а).
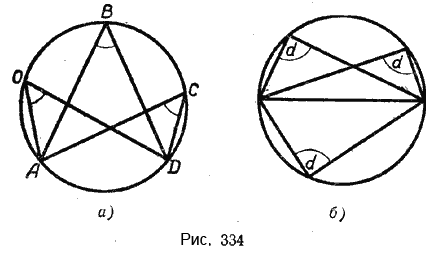
2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности. Половина окружности содержит 180 дуговых градусов, значит, угол, опирающийся на диаметр, содержит 90 угловых градусов (рис. 334, б).