Объем прямой призмы
1. Объём прямой треугольной призмы.
Пусть требуется найти объём прямой треугольной призмы, площадь основания которой равна S, а высота равна h = AA’ = BB’ = CC’ (рис. 306).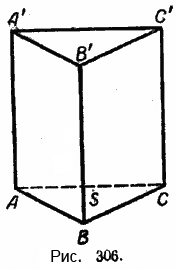
Начертим отдельно основание призмы, т. е. треугольник АBС (рис. 307, а), и достроим его до прямоугольника, для чего через вершину В проведём прямую КМ || АС и из точек A и С опустим на эту прямую перпендикуляры АF и СЕ. Получим прямоугольник АСЕF. Проведя высоту ВD треугольника АBС, увидим, что прямоугольник АСЕF разбился на 4 прямоугольных треугольника. Причём \(\Delta\)ВСЕ = \(\Delta\)BCD и \(\Delta\)BAF = \(\Delta\)BAD. Значит, площадь прямоугольника АСЕF вдвое больше площади треугольника АBС, т. е. равна 2S.
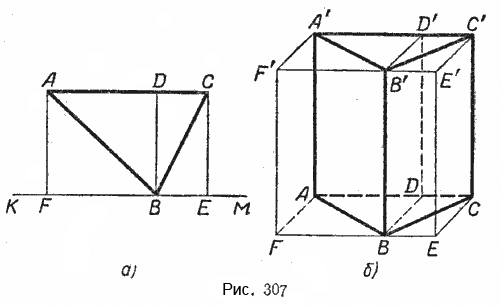
К данной призме с основанием АBС пристроим призмы с основаниями ВСЕ и BАF и высотой h (рис. 307, б). Получим прямоугольный параллелепипед с основанием АСЕF.
Если этот параллелепипед рассечём плоскостью, проходящей через прямые BD и BB’, то увидим, что прямоугольный параллелепипед состоит из 4 призм с основаниями BCD, ВСЕ, BАD и BAF.
Призмы с основаниями BCD и ВСЕ могут быть совмещены, так как основания их равны (\(\Delta\)BCD = \(\Delta\)BСЕ) и также равны их боковые рёбра, являющиеся перпендикулярами к одной плоскости. Значит, объёмы этих призм равны. Также равны объёмы призм с основаниями BАD и BАF.
Таким образом, оказывается, что объём данной треугольной призмы с основанием АBС вдвое меньше объёма прямоугольного параллелепипеда с основанием АСЕF.
Нам известно, что объём прямоугольного параллелепипеда равен произведению площади его основания на высоту, т. е. в данном случае равен 2Sh. Отсюда объём данной прямой треугольной призмы равен Sh.
Объём прямой треугольной призмы равен произведению площади её основания на высоту.
2. Объём прямой многоугольной призмы.
Чтобы найти объём прямой многоугольной призмы, например пятиугольной, с площадью основания Sи высотой h, разобьём её на треугольные призмы (рис. 308).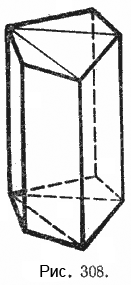
Обозначив площади основания треугольных призм через S1, S2и S3, а объём данной многоугольной призмы через V, получим:
V = S1h + S2h + S3h, или
V = (S1 + S2 + S3)h.
И окончательно: V = Sh.
Таким же путём выводится формула объема прямой призмы, имеющей в основании любой многоугольник.
Значит, объём любой прямой призмы равен произведению площади её основания на высоту.
Объём призмы
Теорема. Объём призмы равен произведению площади основания на высоту.
Сначала докажем эту теорему для треугольной призмы, а потом и для многоугольной.
1) Проведём (черт. 95) через ребро AA1 треугольной призмы АВСА1В1С1 плоскость, параллельную грани ВВ1С1С, а через ребро СС1 - плоскость, параллельную грани AA1B1B; затем продолжим плоскости обоих оснований призмы до пересечения с проведёнными плоскостями.
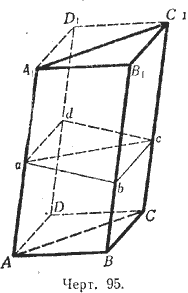
Тогда мы получим параллелепипед BD1, который диагональной плоскостью АА1С1С делится на две треугольные призмы (из них одна есть данная). Докажем, что эти призмы равновелики. Для этого проведём перпендикулярное сечение abcd. В сечении получится параллелограмм, который диагональю ас делится на два равных треугольника. Данная призма равновелика такой прямой призме, у которой основание есть \(\Delta\)аbc, а высота - ребро АА1. Другая треугольная призма равновелика такой прямой, у которой основание есть \(\Delta\)аdс, а высота - ребро АА1. Но две прямые призмы с равными основаниями и равными высотами равны (потому что при вложении они совмещаются), значит, призмы АВСА1В1С1 и ADCA1D1C1 равновелики. Из этого следует, что объём данной призмы составляет половину объёма параллелепипеда BD1; поэтому, обозначив высоту призмы через H, получим:
$$ V_{\Delta пр.} = \frac{S_{ABCD}\cdot H}{2} = \frac{S_{ABCD}}{2}\cdot H = S_{ABC}\cdot H $$2) Проведём через ребро АА1 многоугольной призмы (черт. 96) диагональные плоскости АА1С1С и AA1D1D.
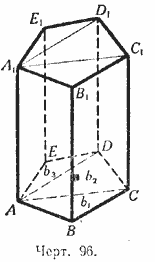
Тогда данная призма рассечётся на несколько треугольных призм. Сумма объёмов этих призм составляет искомый объём. Если обозначим площади их оснований через b1, b2, b3, а общую высоту через Н, то получим:
объём многоугольной призмы = b1• H +b2• H + b3• H =(b1 + b2+ b3 ) • H =
= (площади ABCDE) • H.
Следствие. Если V, В и Н будут числа, выражающие в соответствующих единицах объём, площадь основания и высоту призмы, то, по доказанному, можно написать:
V = BH.