Свойства граней и диагоналей параллелепипеда

Теорема. Во всяком параллелепипеде противоположные грани равны и параллельны.

Так, грани (рис.) BB₁С₁С и AA₁D₁D параллельны, потому, что две пересекающиеся прямые BB₁ и B₁С₁ одной грани параллельны двум пересекающимся прямым AA₁ и A₁D₁ другой. Эти грани и равны, так как B₁С₁=A₁D₁, B₁B=A₁A (как противоположные стороны параллелограммов) и ∠BB₁С₁ = ∠AA₁D₁.

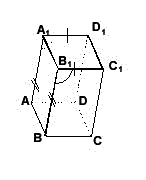
Теорема. Во всяком параллелепипеде все четыре диагонали пересекаются в одной точке и делятся в ней пополам.

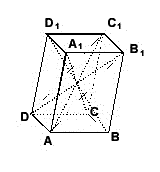
Возьмем (рис.) в параллелепипеде какие-нибудь две диагонали, например, AС₁ и DB₁, и проведем прямые AB₁ и DС₁.

Так как ребра AD и B₁С₁ соответственно равны и параллельны ребру BС, то они равны и параллельны между собой.

Вследствие этого фигура ADС₁B₁ есть параллелограмм, в котором С₁A и DB₁ - диагонали, а в параллелограмме диагонали пересекаются пополам.

Это доказательство можно повторить о каждых двух диагоналях.

Поэтому диагональ AC₁ пересекается с BD₁ пополам, диагональ BD₁ с A₁С пополам.

Таким образом, все диагонали пересекаются пополам и, следовательно, в одной точке.

Теорема. В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.

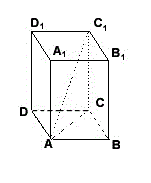
Пусть (рис.) AC₁ есть какая-нибудь диагональ прямоугольного параллелепипеда.

Проведя AC, получим два треугольника: AC₁С и ACB. Оба они прямоугольные:

первый потому, что параллелепипед прямой, и следовательно, ребро СС₁ перпендикулярно к основанию,

второй потому, что параллелепипед прямоугольный, значит в основании его лежит прямоугольник.

Из этих треугольников находим:

AC²₁ = AC² + СС²₁ и AC² = AB² + BC²

Следовательно, AC²₁= AB² + BC² + СС²₁ = AB² + AD² + AA²₁

Следствие. В прямоугольном параллелепипеде все диагонали равны.