Боковая поверхность призмы и пирамиды

Теорема. Боковая поверхность призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

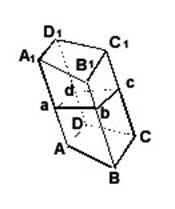
Перпендикулярным сечением (рис.) называется многоугольник abcd, получаемый от пересечения призмы плоскостью, перпендикулярной к боковым ребрам. Стороны этого многоугольника перпендикулярны к ребрам.

Боковая поверхность призмы есть сумма площадей параллелограммов. В каждом из них за основание можно взять боковое ребро, а за высоту сторону перпендикулярного сечения. Поэтому:

Бок. пов. = AA₁ * ab + BB₁ * bс + СС₁ * сd + DD₁ * da = (ab+bс+сd+da) * AA₁

Следствие. Боковая поверхность прямой призмы равна произведению периметра основания на высоту, потому что в такой призме за перпендикулярное сечение можно взять само основание, а боковое ребро ее равно высоте.

Теорема. Боковая поверхность правильной пирамиды равна произведению периметра основания на половину апофемы.

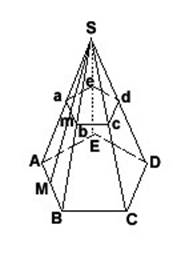
Пусть (рис.) SABCDE есть правильная пирамида и SM ее апофема.

Боковая поверхность этой пирамиды есть сумма площадей равных равнобедренных треугольников.

Площадь одного из них, например ASB, равна AB * 1/2SM.

Если всех треугольников n, то боковая поверхность выразится:

AB * 1/2SM * n = (AB * n) * 1/2SM, где AB * n есть периметр основания, а SM апофема.

Теорема. Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров обоих оснований на апофему.

Эта поверхность есть сумма площадей равных трапеций. Площадь одной из них, например AabB (рис.), равна 1/2 (AB + ab) * Mm.

Если число всех трапеций есть n, то

Бок. пов. = \( \frac{AB+ab}{2} \cdot Mm \cdot n = \frac{AB\cdot n + ab\cdot n}{2}\cdot Mm \)

где AB * n и ab * n - периметры нижнего и верхнего оснований.