Из точки А, расположенной внутри угла с зеркальными сторонами, исходит луч света. Доказать, что число отражений, которое испытывает этот луч от сторон угла, всегда конечно. Найти это число, если данный угол равен α, а луч направлен под углом β к одной из его сторон. Выяснить условия, при которых луч снова пройдет через точку А.

Пусть S — вершина данного угла α, А₁ — точка первой встречи луча с зеркалом, SB₁ — та сторона угла, на которой лежит точка А₁ и SB₀ — другая его сторона. Последующие точки встречи луча со сторонами угла обозначим через А₂, А₃, ..., так что путь луча внутри угла будет иметь вид ломаной AA₁A₂A₃... .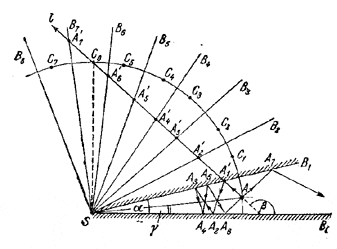

В направлении вращения от SB₀ к SB₁ построим последовательно углы B₁SB₂, B₂SB₃, ..., равные углу α = ∠B₀SB₁. Ha стороне SB_m (m = 2, 3, 4, ...) отложим отрезок SA'_m = SA_m (точки A'₁и A₁совпадают) и докажем, что точки A'₁, A'₂, ... лежат на одной прямой. Для этого достаточно доказать, что каждые три последовательные точки A'_m, A'_m+1, A'_m+2 лежат на одной прямой (мы полагаем здесь m = 0, 1, 2, ...). Для этого заметим, что \(\Delta\)A'_mSA'_m+1 = \(\Delta\)A_mSA_m+1, в силу чего

∠A'_mA'_m+1 S= ∠A_mA_m+1S.

Аналогично \(\Delta\)A'_m+1SA'_m+2 = A_m+1SA_m+2 и, значит,

∠SA'_m+1A'_m+2= ∠SA_m+1A_m+2.

Но по закону отражения (угол падения равен углу отражения)

∠SA_m+1A_m+2= ∠A_mA_m+1В.

Следовательно,

∠A'_mA'_m+1S + ∠SA'_m+1A'_m+2 = ∠A_mA_m+1S + ∠A_mA_m+1В= π.

Таким образом, путь луча — ломаная АА₁А₂...— оказался развернутым в прямую l (АА'₁А'₂...). Так как эта прямая может пересечь лишь конечное число сторон SB_m, то, следовательно, число отражений луча конечно.

Ясно, что если SB_n— последняя из сторон, которую пересекает прямая l, то

пα < β, a (n + 1)α > β. Таким образом, число отражений равно такому целому числу n, которое удовлетворяет неравенствам

n < ^β/_α < n + 1

Для того чтобы выяснить условия, при которых луч после некоторого числа отражений снова пройдет через точку А, построим ряд точек С₁, С₂) ... так, чтобы точка С₁ была симметрична точке А относительно SB₁ точка С₂ симметрична точке C₁ относительно SB₂ и т. д., вообще, чтобы точка С_m была симметрична точке С_m—1 относительно SB_m. Ясно, что прохождение луча снова через точку А равносильно прохождению прямой l через одну из точек С_m (m = 1, 2, ...).

Для аналитической формулировки этого условия введем угол γ = ∠ASB₀ и будем различать два случая:

а) точка С_k через которую проходит прямая l, такова, что k — четное число;

б) точка C_k такова, что k — нечетное число.

В случае а) (этот случай изображен на рис., где k= 6)

∠ASC_k = kα. Так как ∠ASC_k равнобедренный, то

∠ASC_k = ^π/₂ = ^kα/₂

С другой стороны, тот же угол равен γ + π — β. следовательно,

^π/₂ — ^kα/₂= γ + π — β

откуда

(1)

В случае б) будем иметь

∠ASC_k = ( k +1) α — 2γ

и, как и выше, придем к соотношению

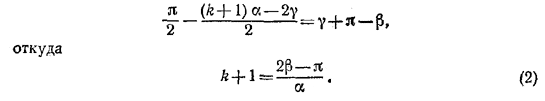
Проведя рассуждение в обратном порядке, легко убедиться в том, что выполнение одного из соотношений (1) или (2) при целом значении k влечет прохождение прямой l через точку С_k . Следовательно, луч снова пройдет через точку А тогда и только тогда, когда одно из чисел (1) или (2) будет целым четным числом.