Доказать, что основания перпендикуляров, опущенных из произвольной точки окружности на стороны вписанного в нее треугольника, лежат на одной прямой.

Пусть ABC — вписанный в окружность треугольник, D — точка окружности, L, М, N — основания перпендикуляров.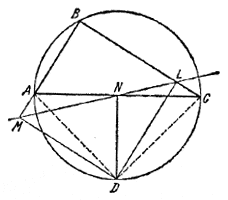

Соединим точки М с N и N с L и докажем, что углы ANM и LNC равны.

Заметим для этого, что

∠ANM = ∠ADM, (1)

так как около четырехугольника MAND можно описать окружность.

По той же причине

∠LNC = ∠LDC; (2)

с другой стороны,

∠ADC = ∠MDL. (3)

Действительно, ∠ADC + ∠В = 180°, так как эти два угла в сумме опираются на полную окружность; в то же время ∠MDL + ∠В = 180°, так как около четырехугольника MBLD можно описать окружность. Следовательно, равенство (3) справедливо. Из чертежа ясно, что в таком случае

∠LDC = ∠ADM,

а тогда из (1) и (2) вытекает равенство

∠ANM = ∠LNC,

которое и требовалось доказать.