Основанием пирамиды служит ромб с острым углом α. Боковые грани наклонены к плоскости основания под углом β. Определить объем и полную поверхность пирамиды, если радиус вписанного в ромб круга равен r.
Прямая LN, соединяющая точки касания L и N противоположных сторон ромба (рис., а), проходит через центр окружности. Поэтому, начертив сначала эллипс (рис., б), изображающий окружность , проведем через центр О две прямые NL и КМ. Через концы их N, L, К, М проведем прямые, касающиеся эллипса. Получим параллелограмм ABCD, изображающий ромб.
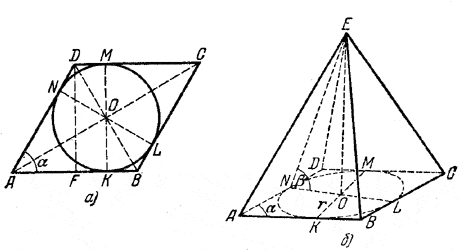
Решение. Чтобы определить Socн., найдем высоту DF и сторону АВ ромба.
Из рис.а находим DF = 2OK = 2r ; из треугольника AFD, где ∠ A = α, имеем
a = AD = DF/sin α = 2r/sin α
Далее находим
![]()
Из треугольника ONE (рис., б), где ОN= r, a ∠ ONE = β , находим H. Для определения Sп. используем замечание к предыдущей задаче.
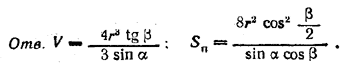
Похожие примеры: