Симметрия фигур в пространстве
Центральная симметрия
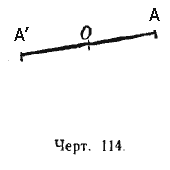
Две фигуры называются симметричными относительно какой-либо точки О пространства, если каждой точке А одной фигуры соответствует в другой фигуре точка А’, расположенная на прямой ОА по другую сторону от точки О, на расстоянии, равном расстоянию точки А от точки О (черт. 114). Точка О называется центром симметрии фигур.
Пример таких симметричных фигур в пространстве мы уже встречали (§ 53), когда, продолжая за вершину рёбра и грани многогранного угла, получали многогранный угол, симметричный данному. Соответственные отрезки и углы, входящие в состав двух симметричных фигур, равны между собой. Тем не менее фигуры в целом не могут быть названы равными: их нельзя совместить одну с другой вследствие того, что порядок расположения частей в одной фигуре иной, чем в другой, как это мы видели на примере симметричных многогранных углов.
В отдельных случаях симметричные фигуры могут совмещаться, но при этом будут совпадать несоответственные их части. Например, возьмём прямой трёхгранный угол (черт. 115) с вершиной в точке О и рёбрами ОХ, OY, OZ.
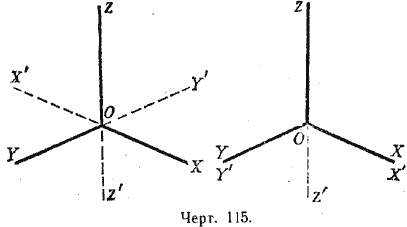
Построим ему симметричный угол ОХ’Y’Z’. Угол OXYZ можно совместить с OX’Y’Z’ так, чтобы ребро ОХ совпало с OY’, а ребро OY c OX’. Если же совместить соответственные рёбра ОХ с ОХ’ и OY с OY’, то рёбра OZ и OZ’ окажутся направленными в противоположные стороны.
Если симметричные фигуры составляют в совокупности одно геометрическое тело, то говорят, что это геометрическое тело имеет центр симметрии. Таким образом, если данное тело имеет центр симметрии, то всякой точке, принадлежащей этому телу, соответствует симметричная точка, тоже принадлежащая данному телу. Из рассмотренных нами геометрических тел центр симметрии имеют, например:
- параллелепипед,
- призма, имеющая в основании правильный многоугольник с чётным числом сторон.
Правильный тетраэдр не имеет центра симметрии.
Симметрия относительно плоскости
Две пространственные фигуры называются симметричными относительно плоскости Р, если каждой точке А в одной фигуре соответствует в другой точка А’, причём отрезок АА’ перпендикулярен к плоскости Р и в точке пересечения с этой плоскостью делится пополам.
Теорема. Всякие два соответственных отрезка в двух симметричных фигурах равны между собой.
Пусть даны две фигуры, симметричные относительно плоскости Р. Выделим две какие-нибудь точки А и В первой фигуры, пусть А’ и В’ - соответствующие им точки второй фигуры (черт. 116, на чертеже фигуры не изображены).
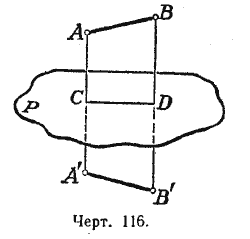
Пусть далее С - точка пересечения отрезка АА’ с плоскостью Р, D - точка пересечения отрезка ВВ’ с той же плоскостью. Соединив прямолинейным отрезком точки С и D, получим два четырёхугольника ABDC и A’B’DC. Так как AС = A’С, BD = B’D и
∠ACD = ∠ACD, ∠BDC = ∠В’DC, как прямые углы, то эти четырёхугольники равны (в чём легко убеждаемся наложением). Следовательно, АВ = А’В’. Из этой теоремы непосредственно вытекает, что соответствующие плоские и двугранные углы двух фигур, симметричных относительно плоскости, равны между собой. Тем не менее совместить эти две фигуры одну с другой так, чтобы совместились их соответственные части, невозможно, так как порядок расположения частей в одной фигуре обратный тому, котoрый имеет место в другой. Простейшим примером двух фигур, симметричных относительно плоскости, являются: любой предмет и его отражение в плоском зеркале; всякая фигура, симметрична со своим зеркальным отражением относительно плоскости зеркала.
Если какое-либо геометрическое тело можно разбить на две части, симметричные относительно некоторой плоскости, то эта плоскость называется плоскостью симметрии данного тела.
Геометрические тела, имеющие плоскость симметрии, чрезвычайно распространены в природе и в обыденной жизни. Тело человека и животного имеет плоскость симметрии, разделяющую его на правую и левую части.
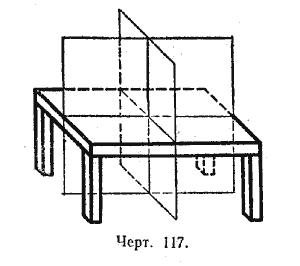
На этом примере особенно ясно видно, что симметричные фигуры нельзя совместить. Так, кисти правой и левой рук симметричны, но совместить их нельзя, что можно видеть хотя бы из того, что одна и та же перчатка не может подходить и к правой и к левой руке. Большое число предметов домашнего обихода имеет плоскость симметрии: стул, обеденный стол, книжный шкаф, диван и др. Некоторые, как например обеденный стол, имеют даже не одну, а две плоскости симметрии (черт. 117).
Обычно, рассматривая предмет, имеющий плоскость симметрии, мы стремимся занять по отношению к нему такое положение, чтобы плоскость симметрии нашего тела, или по крайней мере нашей головы, совпала с плоскостью симметрии самого предмета. В этом случае симметричная форма предмета становится особенно заметной.
Симметрия относительно оси. Ось симметрии второго порядка.
Две фигуры называются симметричными относительно оси l (ось-прямая линия), если каждой точке А первой фигуры соответствует точка А’ второй фигуры, так что отрезок АА’ перпендикулярен к оси l, пересекается с нею и в точке пересечения делится пополам. Сама ось l называется осью симметрии второго порядка.Из этого определения непосредственно следует, что если два геометрических тела, симметричных относительно какой-либо оси, пересечь плоскостью, перпендикулярной к этой оси, то в сечении получатся две плоские фигуры, симметричные относительно точки пересечения плоскости с осью симметрии тел.
Отсюда далее легко вывести, что два тела, симметричных относительно оси, можно совместить одно с другим, вращая одно из них на 180° вокруг оси симметрии. В самом деле, вообразим все возможные плоскости, перпендикулярные к оси симметрии.
Каждая такая плоскость, пересекающая оба тела, содержит фигуры, симметричные относительно точки встречи плоскости с осью симметрии тел. Если заставить скользить секущую плоскость саму по себе, вращая её вокруг оси симметрии тела на 180°, то первая фигура совпадает со второй.
Это справедливо для любой секущей плоскости. Вращение же всех сечений тела на 180° равносильно повороту всего тела на 180° вокруг оси симметрии. Отсюда и вытекает справедливость нашего утверждения.
Если после вращения пространственной фигуры вокруг некоторой прямой на 180° она совпадает сама с собой, то говорят, что фигура имеет эту прямую своею осью симметрии второго порядка.
Название "ось симметрии второго порядка " объясняется тем, что при полном обороте вокруг этой оси тело будет в процессе вращения дважды принимать положение, совпадающее с исходным (считая и исходное). Примерами геометрических тел, имеющих ось симметрии второго порядка, могут служить:
1) правильная пирамида с чётным числом боковых граней; осью её симметрии служит её высота;
2) прямоугольный параллелепипед; он имеет три оси симметрии: прямые, соединяющие центры его противоположных граней;
3) правильная призма с чётным числом боковых граней. Осью её симметрии служит каждая прямая, соединяющая центры любой пары её противоположных граней (боковых граней и двух оснований призмы). Если число боковых граней призмы 2k, то число таких осей симметрии будет k + 1. Кроме того, осью симметрии для такой призмы служит каждая прямая, соединяющая середины её противоположных боковых рёбер. Таких осей симметрии призма имеет А.
Таким образом, правильная 2k-гранная призма имеет 2k+1 осей, симметрии.
Зависимость между различными видами симметрии в пространстве.
Между различными видами симметрии в пространстве - осевой, плоскостной и центральной - существует зависимость, выражаемая следующей теоремой.Теорема. Если фигура F симметрична с фигурой F’ относительно плоскости Р и в то же время симметрична с фигурой F" относительно точки О, лежащей в плоскости Р, то фигуры F’ и F" симметричны относительно оси, проходящей через точку О и перпендикулярной к плоскости Р.
Возьмём какую-нибудь точку А фигуры F (черт. 118). Ей соответствует точка А’ фигуры F’ и точка А" фигуры F" (сами фигуры F, F’ и F" на чертеже не изображены).
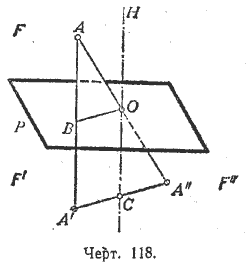
Пусть B - точка пересечения отрезка АА’ с плоскостью Р. Проведeм плоскость через точки А, А’ и О. Эта плоскость будет перпендикулярна к плоскости Р, так как проходит через прямую АА’, перпендикулярную к этой плоскости. В плоскости АА’О проведём прямую ОН, перпендикулярную к ОВ. Эта прямая ОН будет перпендикулярна и к плоскости Р. Пусть далее С-точка пересечения прямых А’А" и ОН.
B треугольнике АА’А" отрезок ВО соединяет середины сторон АА’ и АА", следовательно, ВО || А’А", но ВО⊥ОН, значит, А’А"⊥ОН. Далее, так как О - середина стороны АA", и СО || АА’, то А’С = А"С. Отсюда заключаем, что точки А’ и А" симметричны относительно оси ОН. То же самое справедливо и для всех других точек фигуры. Значит, наша теорема доказана. Из этой теоремы непосредственно следует, что две фигуры, симметричные относительно плоскости, не могут быть совмещены так, чтобы совместились их соответственные части. В самом деле, фигура F’ совмещается с F" путём вращения вокруг оси ОН на 180°. Но фигуры F" и F не могут быть совмещены как симметричные относительно точки, следовательно, фигуры F и F’ также не могут быть совмещены.
Оси симметрии высших порядков
Фигура, имеющая ось симметрии, совмещается сама с собой после поворота вокруг оси симметрии на угол в 180°. Но возможны случаи, когда фигура приходит к совмещению с исходным положением после поворота вокруг некоторой оси на угол, меньший 180°. Таким образом, если тело сделает полный оборот вокруг этой оси, то в процессе вращения оно несколько раз совместится со своим первоначальным положением. Такая ось вращения называется осью симметрии высшего порядка, причём число положений тела, совпадающих с первоначальным, называется порядком оси симметрии. Эта ось может и не совпадать с осью симметрии второго порядка. Так, правильная треугольная пирамида не имеет оси симметрии второго порядка, но её высота служит для неё осью симметрии третьего порядка. В самом деле, после поворота этой пирамиды вокруг высоты на угол в 120° она совмещается сама с собой (черт. 119).
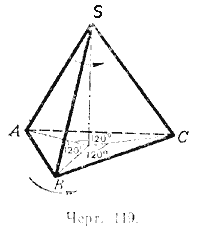
При вращении пирамиды вокруг высоты она может занимать три положения, совпадающие с исходным, считая и исходное. Легко заметить, что всякая ось симметрии чётного порядка есть в то же время ось симметрии второго порядка.
Примеры осей симметрии высших порядков:
1) Правильная n-угольная пирамида имеет ось симметрии n-го порядка. Этой осью служит высота пирамиды.
2) Правильная n-угольная призма имеет ось симметрии n-го порядка. Этой осью служит прямая, соединяющая центры оснований призмы.
Симметрия куба.
Как и для всякого параллелепипеда, точка пересечения диагоналей куба есть центр его симметрии.Куб имеет девять плоскостей симметрии: шесть диагональных плоскостей и три плоскости, проходящие через середины каждой четвёрки его параллельных рёбер.
Куб имеет девять осей симметрии второго порядка: шесть прямых, соединяющих середины его противоположных рёбер, и три прямые, соединяющие центры противоположных граней (черт. 120).
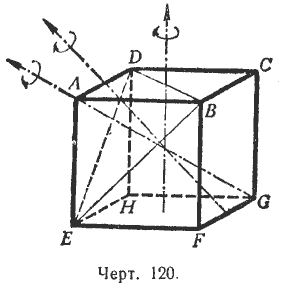
Эти последние прямые являются осями симметрии четвёртого порядка. Кроме того, куб имеет четыре оси симметрии третьего порядка, которые являются его диагоналями. В самом деле, диагональ куба АG (черт. 120), очевидно, одинаково наклонена к рeбрам АВ, АD и АЕ, а эти рёбра одинаково наклонены одно к другому. Ecли соединить точки В, D и Е, то получим правильную треугольную пирамиду АDВЕ, для которой диагональ куба AG служит высотой. Когда при вращении вокруг высоты эта пирамида будет совмещаться сама с собой, весь куб будет совмещаться со своим исходным положением. Других осей симметрии, как нетрудно убедиться, куб не имеет. Посмотрим, сколькими различными способами куб может быть совмещён сам с собой. Вращение вокруг обыкновенной оси симметрии даёт одно положение куба, отличное от исходного, при котором куб в целом совмещается сам с собой.
Вращение вокруг оси третьего порядка даёт два таких положения, и вращение вокруг оси четвёртого порядка - три таких положения. Так как куб имеет шесть осей второго порядка (это обыкновенные оси симметрии), четыре оси третьего порядка и три оси четвёртого порядка, то имеются 6•1 + 4•2 + 3•3 = 23 положения куба, отличные от исходного, при которых он совмещается сам с собой.
Легко убедиться непосредственно, что все эти положения отличны одно от другого, а также и от исходного положения куба. Вместе с исходным положением они составляют 24 способа совмещения куба с самим собой.