Основные аксиомы стереометрии и следствия из них
Раздел геометрии, в котором изучаются фигуры, расположенные в пространстве, называется стереометрией.
Основными понятиями стереометрии являются точка, прямая и плоскость. Пространство состоит из бесконечного множества точек. Прямые и плоскости состоят из бесконечного множества точек пространства и не совпадают со всем пространством.
Сформулируем основные аксиомы стереометрии. Напомним, аксиомы - это предложения, принимаемые без доказательства. Аксиомы геометрии являются абстракцией соответствующих свойств окружающего нас реального мира.
Будем предполагать, что для любой плоскости пространства выполняются все аксиомы, определения и теоремы планиметрии. Кроме того, будем предполагать справедливыми следующие аксиомы стереометрии:
1. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.
2. Если две различные точки прямой принадлежат плоскости, то все точки прямой принадлежат этой плоскости.
3. Если две различные плоскости пересекаются, то они пересекаются по прямой.
Используя эти аксиомы, докажем следующие утверждения:
Следствие 1. Через прямую и не принадлежащую ей точку проходит единственная плоскость.
Доказательство. На данной прямой l возьмем какие-нибудь две точки А и В (рис.).
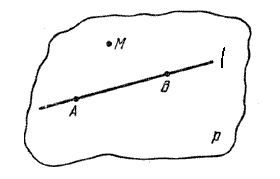
Тогда по аксиоме 1 через данную точку М и точки А и В проходит единственная плоскость р и все точки прямой l принадлежат плоскости р.
Следовательно, плоскость р проходит через прямую l и не принадлежащую ей точку М. Другой такой плоскости нет, так как она должна проходить через три точки А, В, М, не лежащие на одной прямой, и, следовательно, должна совпасть с плоскостью р.
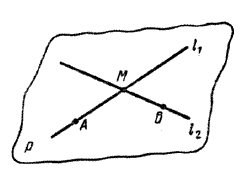
Следствие 2. Через две пересекающиеся прямые проходит единственная плоскость.
Доказательство. Действительно, пусть прямые 11 и 12 пересекаются в точке М (рис.).