Расстояние между двумя точками на плоскости

Каждая точка А плоскости характеризуется своими координатами (х, у). Они совпадают с координатами вектора 0А, выходящего из точки 0 - начала координат .

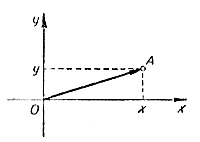
Пусть А и В - произвольные точки плоскости с координатами (х₁ y₁) и (х₂, у₂) соответственно.

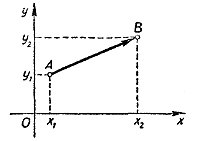
Тогда вектор AB имеет, очевидно, координаты (х₂ - х₁, y₂ - y₁). Известно, что квадрат длины вектора равен сумме квадратов его координат. Поэтому расстояние d между точками А и В, или, что то же самое, длина вектора АВ, определяется из условия

d² = (х₂ - х₁)² + (y₂ - y₁)².

Отсюда

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$

Полученная формула позволяет находить расстояние между любыми двумя точками плоскости, если только известны координаты этих точек

Каждый раз, говоря о координатах той или иной точки плоскости, мы имеем в виду вполне определенную систему координат х0у. А вообще-то систему координат на плоскости можно выбирать по-разному. Так, вместо системы координат х0у можно рассмотреть систему координат хִу’ , которая получается в результате поворота старых осей координат вокруг начальной точки 0 против часовой стрелки на угол α.

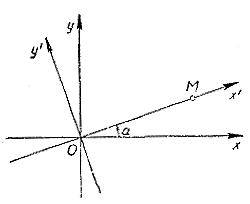
Если некоторая точка плоскости в системе координат х0у имела координаты (х, у), то в новой системе координат хִу’ она будет иметь уже другие координаты (х’, у’).

В качестве примера рассмотрим точку М, расположенную на оси 0х’ и отстоящую от точки 0 на расстоянии, равном 1.

Очевидно, что в системе координат x0у эта точка имеет координаты (cos α, sin α), а в системе координат хִу’ координаты (1,0).

Координаты любых двух точек плоскости А и В зависят от того, как в этой плоскости задана система координат. А вот расстояние между этими точками не зависит от способа задания системы координат.