Доказать, что геометрическое место точек М, расстояния которых до двух данных точек А и В находятся в данном отношении

^p/_q=/= 1 есть окружность с центром на прямой АВ. Выразить диаметр этой окружности через длину a отрезка АВ. Исследовать также случай

^p/_q= 1

Пусть

Проведем биссектрисы МР и MQ двух смежных углов с вершиной М и сторонами МА и MB (рис.).

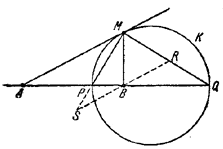
Тогда по свойству биссектрис будем иметь:

Отсюда следует, что положение точек Р и Q не зависит от положения точки М. Так как, кроме того, ∠PMQ = ^π/₂ , то точка М лежит на окружности К с диаметром PQ. Обратно, пусть точки Р и Q построены согласно (1) и К-окружность с диаметром PQ. Если точка М лежит на этой окружности, то ∠PMQ = ^π/₂ .

Через точку В проведем RS ||AM, тогда

откуда BR = BS и ВМ - медиана в \(\Delta\)RMS. Так как \(\Delta\)RMS - прямоугольный, то BM=BR и в силу (2)

Поэтому точка М принадлежит рассматриваемому геометрическому месту.

Чтобы выразить диаметр PQ через длину a отрезка АВ из соотношений

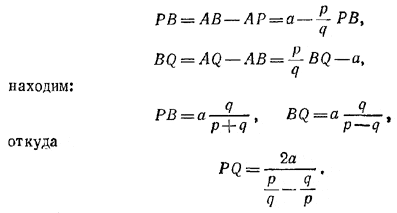
Если p = q, то искомым геометрическим местом будет, очевидно, перпендикуляр к прямой АВ, проведенный через середину отрезка АВ.