Найти геометрическое место точек, для которых сумма расстояний до двух данных прямых m и l равна длине a данного отрезка. Разобрать случаи пересекающихся и параллельных прямых.

В случае пересекающихся прямых искомое геометрическое место состоит из четырех отрезков, образующих прямоугольник ABCD, вершины которого лежат на данных прямых l , m и находятся от них на данном расстоянии a.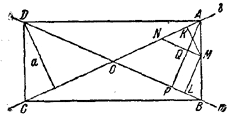

Доказательство. Пусть точка М такова, что МК ⊥ l, ML⊥m и MK + ML = a, где a -длина данного отрезка.

Проведем через М прямую АВ так, чтобы ОА = ОВ и MN || ОВ. Пусть АР⊥ОВ и Q- точка пересечения АР и MN. Из равенства AN = MN следует, что MK = AQ и, значит,

AP = AQ + QP = MK + ML = a.

Следовательно, точка А является вершиной упомянутого прямоугольника. То же верно и для точки В, так что М лежит на стороне этого прямоугольника. Обратно, если М лежит на стороне этого прямоугольника, то, проведя рассуждение в обратном порядке, получим, что MK+ ML = AP = a.

Если данные прямые l и m параллельны и расстояние между ними равно h, то искомое геометрическое место существует только тогда, когда a > h, и представляет собой пару прямых, параллельных данным, при а > h или всю полосу между l и m при a = h.