Площадь трапеции

Пусть нам нужно узнать, чему равняется площадь трапеции АВСD (черт. 278).

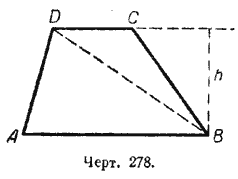
Проведём в ней диагональ DВ. Трапеция разобьётся на два треугольника АDВ и DСВ. Обозначим высоту трапеции и треугольников через h, а площади треугольников АDВ и DВС - через S₁, и S₂. Тогда

$$ S_1 = \frac{ABh}{2}; \;\; S_2 = \frac{DCh}{2} $$

Следовательно, площадь всей трапеции выразится так:

$$ S_{ABCD} = \frac{ABh}{2} + \frac{DCh}{2} = \frac{(AB + DC)\cdot h}{2} = \frac{AB + DC}{2} : h $$

Площадь трапеции равна произведению полусуммы её оснований на высоту.

\( \bf S_{трапеции} = \frac{a + b}{2} \cdot h \),

где а и b- основания трапеции, а h - её высота.