Объем пирамиды
Теорема. Объём пирамиды равен произведению площади её oснования на треть её высоты.
Сначала докажем эту теорему для пирамиды треугольной, а затем и многоугольной.
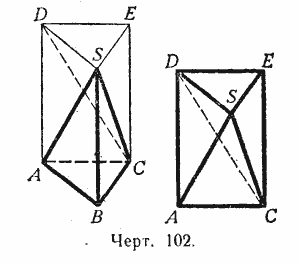
1) На основании треугольной пирамиды SABC (черт. 102) построим такую призму SABCDE, у которой высота равна высоте пирамиды, а одно боковое ребро совпадает с ребром SB. Докажем, что объём пирамиды составляет третью часть объёма этой призмы. Отделим от призмы данную пирамиду. Тогда останется четырёхугольная пирамида SADEC (которая для ясности изображена отдельно). Проведём в ней секущую плоскость через вершину S и диагональ основания DC. Получившиеся от этого две треугольные пирамиды имеют общую вершину S и равные основания DEC и DAC, лежащие в одной плоскости; значит, согласно доказанной выше лемме пирамиды эти равновелики. Сравним одну из них, именно SDEC, с данной пирамидой. За основание пирамиды SDEC можно взять \(\Delta\)SDE; тогда вершина её будет в точке С и высота равна высоте данной пирамиды. Так как \(\Delta\)SDE = \(\Delta\)АВС, то согласно той же лемме пирамиды SDEC и SABC равновелики.
Призма ABCDES нами разбита на три равновеликие пирамиды: SABC, SDEC и SDAC. (Такому разбиению, очевидно, можно подвергнуть всякую треугольную призму. Это является одним из важных свойств треугольной призмы.) Таким образом, сумма объёмов трёх пирамид, равновеликих данной, составляет объём призмы; следовательно,
$$ V_{SABC} = \frac{1}{3} V_{SDEABC} = \frac{S_{ABC}\cdot H}{3} = S_{ABC}\frac{H}{3} $$где Н есть высота пирамиды.
2) Через какую-нибудь вершину Е (черт. 103) основания многоугольной пирамиды SABCDE проведём диагонали ЕВ и ЕС.
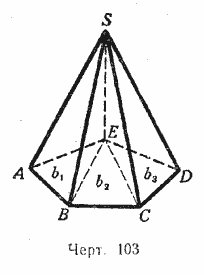
Затем через ребро SE и каждую из этих диагоналей проведём секущие плоскости. Тогда многоугольная пирамида разобьётся на несколько треугольных, имеющих высоту, общую с данной пирамидой. Обозначив площади оснований треугольных пирамид через b1, b2 , b3 и высоту через Н, будем иметь:
объём SABCDE = 1/3 b1• H + 1/3 b2• H + 1/3 b3• H = (b1 + b2 + b3) • H/3 =
= (площади ABCDE) • H/3.
Следствие. Если V, В и Н означают числа, выражающие в соответствующих единицах объём, площадь основания и высоту какой угодно пирамиды, то
V = 1/3 BH
Теорема. Объём усечённой пирамиды равен сумме объёмов трёх пирамид, имеющих высоту, одинаковую с высотой усечённой пирамиды, а основаниями: одна - нижнее основание данной пирамиды, другая - верхнее основание, а площадь основания третьей пирамиды равна среднему геометрическому площадей верхнего и нижнего оснований.
Пусть площади оснований усечённой пирамиды (черт. 104) будут В и b, высота Н и объём V (усечённая пирамида может быть треугольная или многоугольная - всё равно).
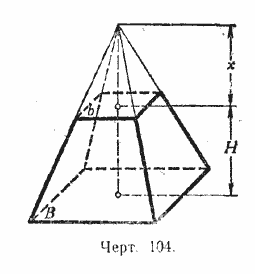
Требуется доказать, что
V = 1/3 BH + 1/3 bH + 1/3 H √Bb = 1/3 H (B + b + √Bb),
где √Bb есть среднее геометрическое между B и b.
Для доказательства на меньшем основании поместим малую пирамиду, дополняющую данную усеченную пирамиду до полной. Тогда объём усечённой пирамиды V мы можем рассматривать как разность двух объёмов - полной пирамиды и верхней дополнительной.
Обозначив, высоту дополнительной пирамиды буквой х, мы найдём, что
V = 1/3 B (Н + х) - 1/3 bх = 1/3( BH + Bх - bх) = 1/3 [ВH + (В - b)х].
Для нахождения высоты х воспользуемся теоремой из раздела, согласно которой мы можем написать уравнение:
$$ \frac{B}{b} = \frac{(H + x)^3}{x^2} $$Для упрощения этого уравнения извлечём из обеих частей его арифметический квадратный корень:
$$ \frac{\sqrt{B}}{\sqrt{b}} = \frac{H + x}{x} $$Из этого уравнения (которое можно рассматривать как пропорцию) получим:
$$ x\sqrt{B} = H\sqrt{b} + x\sqrt{b} $$откуда
$$ (\sqrt{B} - \sqrt{b})x = H\sqrt{b} $$и, следовательно,
$$ x = \frac{H\sqrt{b}}{\sqrt{B} - \sqrt{b}} $$Подставив это выражение в формулу, выведенную нами для объёма V, найдём:
$$ V = \frac{1}{3}\left[BH + \frac{(B-b)H\sqrt{b}}{\sqrt{B} - \sqrt{b}} \right] $$Так как В - b = (√B + √b ) (√B - √b ), то по сокращении дроби на разность √B - √b получим:
$$ V = \frac{1}{3} BH +(\sqrt{B} + \sqrt{b})H\sqrt{b} =\\= \frac{1}{3}(BH+H\sqrt{Bb}+Hb) =\\= \frac{1}{3}H(B+b+\sqrt{Bb}) $$т. е. получим ту формулу, которую требовалось доказать.