Пирамида и усеченная пирамида

Как можно построить пирамиду? На плоскости р построим какой-либо многоугольник, например пятиугольник ABCDE. Вне плоскости р возьмем точку S. Соединив точку S отрезками со всеми точками многоугольника, получим пирамиду SABCDE (рис.).

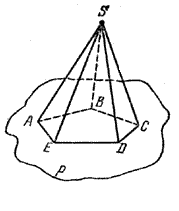
Точка S называется вершиной, а многоугольник ABCDE — основанием этой пирамиды. Таким образом, пирамида с вершиной S и основанием ABCDE — это объединение всех отрезков [SM], где М ∈ ABCDE.

Треугольники SAB, SBC, SCD, SDE, SEA называются боковыми гранями пирамиды, общие стороны боковых граней SA, SB, SC, SD, SE — боковыми ребрами.

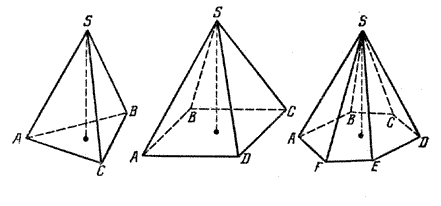
Пирамиды называются треугольными, четырехугольными, п-угольными в зависимости от числа сторон основания. На рис. даны изображения треугольной, четырехугольной и шестиугольной пирамид.

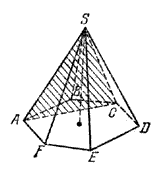
Плоскость, проходящая через вершину пирамиды и диагональ основания, называется диагональной, а полученное сечение — диагональным. На рис. 186 одно из диагональных сечений шестиугольной пирамиды заштриховано.

Отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания, называется высотой пирамиды (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Пирамида называется правильной, если основание пирамиды—правильный многоугольник и вершина пирамиды проектируется в его центр.

Все боковые грани правильной пирамиды — конгруэнтные равнобедренные треугольники. У правильной пирамиды все боковые ребра конгруэнтны.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды. Все апофемы правильной пирамиды конгруэнтны.

Если обозначить сторону основания через а, а апофему через h, то площадь одной боковой грани пирамиды равна ¹/₂ ah .

Сумма площадей всех боковых граней пирамиды называется площадью боковой поверхности пирамиды и обозначается через S_бок.

Так как боковая поверхность правильной пирамиды состоит из n конгруэнтных граней, то

S_бок. = ¹/₂ ahn = ^Ph/₂,

где Р — периметр основания пирамиды. Следовательно,

S_бок. = ^Ph/₂

т. е. площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Площадь полной поверхности пирамиды вычисляется по формуле

S = S_ocн. + S_бок..

Объем пирамиды равен одной трети произведения площади ее основания S_ocн. на высоту Н:

V = ¹/₃ S_ocн. Н.

Вывод этой и некоторых других формул будет дан в одной из последующих глав.

Построим теперь пирамиду другим способом. Пусть дан многогранный угол, например, пятигранный, с вершиной S (рис.).

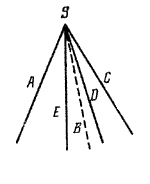
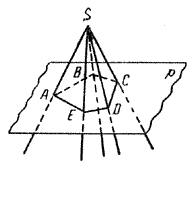
Проведем плоскость р так, чтобы она пересекала все ребра данного многогранного угла в разных точках А, В, С, D, Е (рис.). Тогда пирамиду SABCDE можно рассматривать как пересечение многогранного угла и полупространства с границей р, в котором лежит вершина S.

Очевидно, что число всех граней пирамиды может быть произвольным, но не меньшим четырех. При пересечении трехгранного угла плоскостью получается треугольная пирамида, у которой четыре грани. Любую треугольную пирамиду иногда называют тетраэдром, что означает четырехгранник.

Усеченную пирамиду можно получить, если пирамиду пересечь плоскостью, параллельной плоскости основания.

На рис. дано изображение четырехугольной усеченной пирамиды.

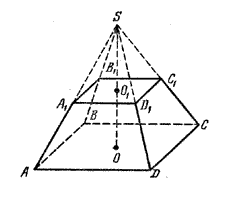
Усеченные пирамиды также называются треугольными, четырехугольными, n-угольными в зависимости от числа сторон основания. Из построения усеченной пирамиды следует, что она имеет два основания: верхнее и нижнее. Основания усеченной пирамиды — два многоугольника, стороны которых попарно параллельны. Боковые грани усеченной пирамиды — трапеции.

Высотой усеченной пирамиды называется отрезок перпендикуляра, проведенного из любой точки верхнего основания к плоскости нижнего.

Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и плоскостью сечения, параллельной основанию. Высота боковой грани правильной усеченной пирамиды (трапеции) называется апофемой.

Можно доказать, что у правильной усеченной пирамиды боковые ребра конгруэнтны, все боковые грани конгруэнтны, все апофемы конгруэнтны.

Если в правильной усеченной n-угольной пирамиде через а и b_n обозначить длины сторон верхнего и нижнего оснований, а через h — длину апофемы, то площадь каждой боковой грани пирамиды равна

¹/₂( а + b_n ) h

Сумма площадей всех боковых граней пирамиды называется площадью ее боковой поверхности и обозначается S_бок. . Очевидно, что для правильной усеченной n-угольной пирамиды

S_бок. = n • ¹/₂( а + b_n ) h .

Так как па = Р и nb_n = Р₁ — периметры оснований усеченной пирамиды, то

S_бок. = ¹/₂ (Р + Р₁) h ,

т. е. площадь боковой поверхности правильной усеченной пирамиды равна половине произведения суммы периметров ее оснований на апофему.

Сечение, параллельное основанию пирамиды

Теорема. Если пирамиду пересечь плоскостью, параллельной основанию, то:

1) боковые ребра и высота разделятся на пропорциональные части;

2) в сечении получится многоугольник, подобный основанию;

3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Теорему достаточно доказать для треугольной пирамиды.

Так как параллельные плоскости пересекаются третьей плоскостью по параллельным прямым, то (АВ) || (А₁В₁), (BС) ||( В₁C₁), (AС) || (A₁С₁) (рис.).

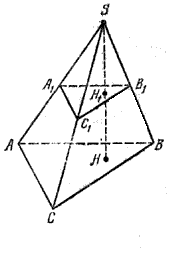
Параллельные прямые рассекают стороны угла на пропорциональные части, и поэтому

$$ \frac{\left|{SA}\right|}{\left|{SA_1}\right|}=\frac{\left|{SB}\right|}{\left|{SB_1}\right|}=\frac{\left|{SC}\right|}{\left|{SC_1}\right|} $$

Следовательно, ΔSAB ~ ΔSA₁B₁ и

$$ \frac{\left|{AB}\right|}{\left|{A_{1}B_1}\right|}=\frac{\left|{SB}\right|}{\left|{SB_1}\right|} $$

ΔSBC ~ ΔSB₁C₁ и

$$ \frac{\left|{BC}\right|}{\left|{B_{1}C_1}\right|}=\frac{\left|{SB}\right|}{\left|{SB_1}\right|}=\frac{\left|{SC}\right|}{\left|{SC_1}\right|} $$

Таким образом,

$$ \frac{\left|{AB}\right|}{\left|{A_{1}B_1}\right|}=\frac{\left|{BC}\right|}{\left|{B_{1}C_1}\right|}=\frac{\left|{AC}\right|}{\left|{A_{1}C_1}\right|} $$

Соответственные углы треугольников ABC и A₁B₁C₁ конгруэнтны, как углы с параллельными и одинаково направленными сторонами. Поэтому

ΔABC ~ ΔA₁B₁C₁

Площади подобных треугольников относятся, как квадраты соответствующих сторон:

$$ \frac{S_{ABC}}{S_{A_1 B_1 C_1}}=\frac{\left|{AB}\right|^2}{\left|{A_{1}B_1}\right|^2} $$

но

$$ \frac{\left|{AB}\right|}{\left|{A_{1}B_1}\right|}=\frac{\left|{SH}\right|}{\left|{SH_1}\right|} $$

Следовательно,

$$ \frac{S_{ABC}}{S_{A_1 B_1 C_1}}=\frac{\left|{SH}\right|^2}{\left|{SH_1}\right|^2} $$

Теорема. Если две пирамиды с равными высотами рассечены на одинаковом расстоянии от вершины плоскостями, параллельными основаниям, то площади сечений пропорциональны площадям оснований.

Пусть (черт. 84) В и В₁— площади оснований двух пирамид, H — высота каждой из них, b и b₁ — площади сечений плоскостями, параллельными основаниям и удалёнными от вершин на одно и то же расстояние h.

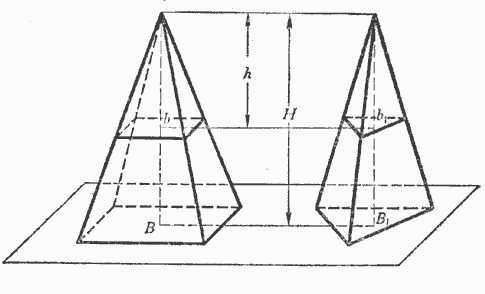
Согласно предыдущей теореме мы будем иметь:

$$ \frac{b}{B}=\frac{h^2}{H^2}\: и \: \frac{b_1}{B_1}=\frac{h^2}{H^2} $$
откуда
$$ \frac{b}{B}=\frac{b_1}{B_1}\:  или \: \frac{b}{b_1}=\frac{B}{B_1} $$

Следствие. Если В = В₁, то и b = b₁ , т. е. если у двух пирамид с равными высотами основания равновелики, то равновелики и сечения, равноотстоящие от вершины.