Свойства правильных многоугольников
Теорема 1. Около любого правильного многоугольника можно описать окружность.
Пусть ABCDEF (рис. 419) - правильный многоугольник; надо доказать, что около него можно описать окружность.
Мы знаем, что всегда можно провести окружность через три точки, не лежащие на одной прямой; значит, всегда можно провести окружность, которая пройдёт через три любые вершины правильного многоугольника, например через вершины Е, D и С. Пусть точка О - центр этой окружности.
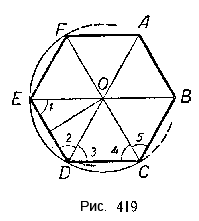
Докажем, что эта окружность пройдёт и через четвёртую вершину многоугольника, например через вершину В.
Отрезки ОЕ, OD и ОС равны между собой, и каждый равен радиусу окружности. Проведём ещё отрезок ОВ; про этот отрезок сразу нельзя сказать, что он также равен радиусу окружности, это надо доказать. Рассмотрим треугольники OED и ODC, они равнобедренные и равные, следовательно, ∠1 = ∠2 = ∠3 = ∠4.
Если внутренний угол данного многоугольника равен α , то ∠1 = ∠2 = ∠3 = ∠4 = α/2 ; но если ∠4= α/2, то и ∠5 = α/2, т.е. ∠4 = ∠5.
Отсюда заключаем, что (Delta)ОСD = (Delta)ОСВ и, значит, ОВ = ОС, т. е. отрезок ОВ равен радиусу проведённой окружности. Из этого следует, что окружность пройдёт и через вершину В правильного многоугольника.
Таким же приёмом докажем,что построенная окружность пройдёт и через все остальные вершины многоугольника. Значит, эта окружность будет описанной около данного правильного многоугольника. Теорема доказана.
Теорема 2. В любой правильный многоугольник можно вписать окружность.
Пусть ABCDEF - правильный многоугольник (рис. 420), надо доказать, что в него можно вписать окружность.
Из предыдущей теоремы известно, что около правильного многоугольника можно описать окружность. Пусть точка О - центр этой окружности.
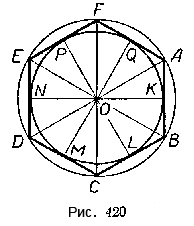
Соединим точку Oс вершинами многоугольника. Полученные треугольники OED, ODC и т д. равны между собой, значит, равны и их высоты, проведённые из точки О, т. е. OK = OL = ОМ = ON = OP = OQ.
Поэтому окружность, описанная из точки О как из центра радиусом, равным отрезку ОК, пройдёт через точки К, L, M, N, Р и Q, и высоты треугольников будут радиусами окружности. Стороны многоугольника перпендикулярны к радиусам в этих точках, поэтому они являются касательными к этой окружности. А это значит, что построенная окружность вписана в данный правильный многоугольник.
Такое же построение можно выполнить для любого правильного многоугольника, следовательно, вписать окружность можно в любой правильный многоугольник.
Следствие. Окружности, описанная около правильного многоугольника и вписанная в него, имеют общий центр.
Определения.
1. Центром правильного многоугольника называется общий центр окружностей, описанной около этого многоугольника и вписанной в него.
2. Перпендикуляр, опущенный из центра правильного многоугольника на его сторону, называется апофемой правильного многоугольника.
Выражение сторон правильных многоугольников через радиус описанной окружности
С помощью тригонометрических функций можно выразить сторону любого правильного многоугольника через радиус описанной около него окружности.
Пусть АВ — сторона правильного n-угольника, вписанного в круг радиуса ОА = R (рис).
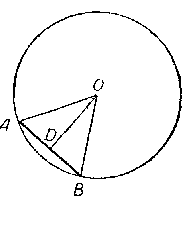
Проведём апофему OD правильного многоугольника и рассмотрим прямоугольный треугольник AOD. В этом треугольнике
∠AOD = 1/2 ∠AOB = 1/2• 360°/n = 180°/n
AD = AO• sin ∠AOD = R sin 180°/n;
но AB = 2AD и потому АВ = 2R sin 180°/n.
Длина стороны правильного n-угольника, вписанного в круг, обозначается обычно аn, поэтому полученную формулу можно записать так:
аn = 2R sin 180°/n.
Следствия:
1. Длина стороны правильного шестиугольника, вписанного в круг радиуса R, выражается формулой а6 = R, так как
а6 = 2R sin 180°/6 = 2R sin 30° = 2R1/2 = R.
2. Длина стороны правильного четырёхугольника (квадрата), вписанного в круг радиуса R, выражается формулой а4 = R √2 , так как
а4 = 2R sin 180°/4 = 2R sin 45° = 2R√2/2 = R√2
3. Длина стороны правильного треугольника, вписанного в круг радиуса R, выражается формулой а3 = R √3 , так как .
а3 = 2R sin 180°/3 = 2R sin 60° = 2R√3/2 = R√3
Площадь правильного многоугольника
Пусть дан правильный n-угольник (рис). Требуется определить его площадь. Обозначим сторону многоугольника через а и центр через О. Соединим отрезками центр с концами какой-либо стороны многоугольника, получим треугольник, в котором проведём апофему многоугольника.
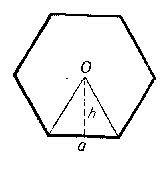
Площадь этого треугольника равна ah/2 . Чтобы определить площадь всего многоугольника нужно площадь одного треугольника умножить на число треугольников, т. е. на n. Получим: S = ah/2 • n = ahn/2, но аn равняется периметру многоугольника. Обозначим его через Р.
Окончательно получаем: S = Ph/2. где S — площадь правильного многоугольника, Р — его периметр, h — апофема.
Площадь правильного многоугольника равна половине произведения его периметра на апофему.