Прямоугольник

Построим прямой угол А. Обозначим на его сторонах две произвольные точки В и С (рис. 235). Через точку В проведём прямую, параллельную АС, а через точку С проведём прямую, параллельную AB.

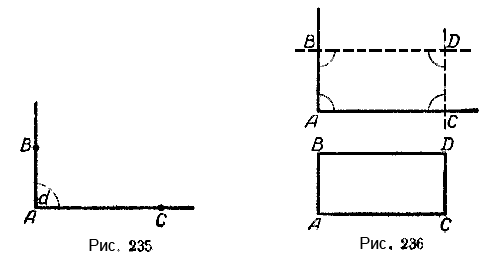
Точку пересечения этих прямых обозначим буквой D (рис.236). Мы получили параллелограмм ABDС, в котором ∠А = 90°. Нетрудно доказать, что в этом параллелограмме все внутренние углы будут прямые.

В самом деле, ∠В + ∠А = 180°, как углы внутренние односторонние при параллельных прямых АС и ВD и секущей AB. Но ∠А = 90°, следовательно, и ∠В = 90°. Кроме того, ∠A = ∠D и ∠В = ∠С, как противоположные углы параллелограмма. Таким образом, все углы этого параллелограмма прямые.

Параллелограмм, у которого все углы прямые, называется прямоугольником.

2. Свойства прямоугольника.

Так как прямоугольник есть параллелограмм, то он обладает всеми его свойствами.

1. Диагональ прямоугольника делит его на два равных треугольника.

2. Диагонали прямоугольника в точке их пересечения делятся пополам.

3. Противоположные стороны прямоугольника равны между собой, равны также и противоположные его углы.

Кроме этих свойств, прямоугольник обладает еще следующим свойством:

Диагонали прямоугольника равны.

Докажем это свойство. Возьмём прямоугольник ABCD, проведём в нём две диагонали (рис. 237) АС и ВD и докажем, что они равны между собой.

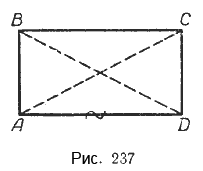
Сравним два треугольника АВD и АСD. Сторона АD у них общая и AB = DС. Кроме того, они прямоугольные. Следовательно, они равны между собой, поэтому АС = ВD.