Средняя линия трапеции
Четырёхугольник, у которого две противоположные стороны параллельны, а другие две - не параллельны, называется трапецией.
На чертеже 252 у четырёхугольника АВDС АВ || СD, AC ||BD. АВDС — трапеция.
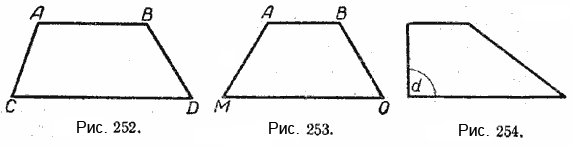
Параллельные стороны трапеции называются её основаниями; АВ и СD — основания трапеции. Остальные две стороны называются боковыми сторонами трапеции; АС и ВD — боковые стороны трапеции.
Если боковые стороны равны, то трапеция называется равнобедренной.
Трапеция АВОМ равнобедренная, так как АМ=ВО (рис. 253).
Трапеция, у которой одна из боковых сторон перпендикулярна к основанию, называется прямоугольной (рис. 254).
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.
Дано: ОС — средняя линия трапеции АВDК, т. е. ОК = ОА и ВС = СD (рис. 255).
Надо доказать:
1) ОС || КD и ОС || АВ;
2) OC = \(\frac{KD + AB}{2}\)
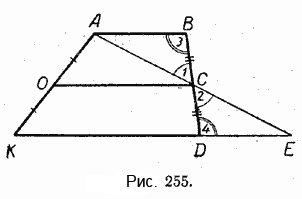
Доказательство. Через точки А и С проведём прямую, пересекающую продолжение основания КD в некоторой точке Е.
В треугольниках АBС и DСЕ:
ВС = СD — по условию;
∠1 = ∠2, как вертикальные,
∠4 = ∠3, как внутренние накрест лежащие при параллельных АВ и KЕ и секущей ВD. Следовательно, \(\Delta\)АBС = \(\Delta\)DСЕ.
Отсюда АС = СЕ, т.е. ОС является средней линией треугольника КАЕ. Следовательно:
1) ОС || КЕ и, значит, ОС || КD и ОС || AВ;
2) OC = \(\frac{KE}{2} = \frac{KD + DE}{2}\), но DЕ = АВ (из равенства треугольников АBС и DСЕ), поэтому отрезок DЕ можно заменить равным ему отрезком АВ. Тогда получим:
OC = \(\frac{KD + AB}{2}\)
Теорема доказана.
Свойства трапеции, которые часто используются при решении задач:
- Диагонали трапеции разбивают её начетыре треугольника с общей вершиной. Площади треугольников, прилежащие к боковым сторонам, равны.
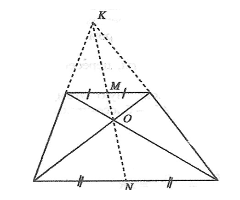
- В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которой лежат боковые стороны, лежат на одной прямой (точки М, N, О и К).
- В равнобокой трапеции углы при основании равны.
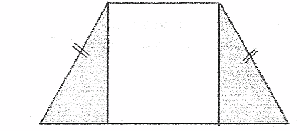
- В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии этой трапеции
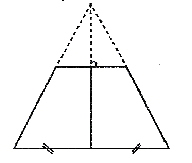
- В равнобокой трапеции диагонали равны.
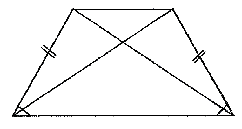
- В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой - их полусумме.
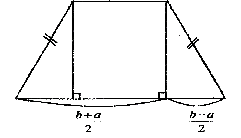
- Во всякой трапеции серединам боковых сторон и середины диагоналей лежат на одной прямой.
- Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований.
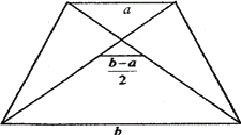
- Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований.
- Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
- Трапецию можно описать около окружности тогда и только тогда, когда сумма оснований равна сумме боковых сторон.