Куб пересекается плоскостью, проходящей через одну из его диагоналей. Как должна быть проведена эта плоскость, чтобы площадь сечения получилась наименьшей?
Не нарушая общности, можно считать, что секущая плоскость пересекается с ребром куба СЕ.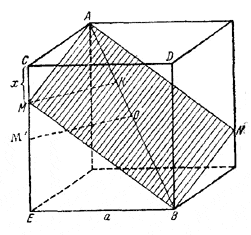
Легко видеть, что в сечении всегда получается некоторый параллелограмм AMBN. Площадь S параллелограмма может быть найдена по формуле
S = AB•MK,
где через МК обозначен перпендикуляр, опущенный из точки М ребра СЕ на диагональ АВ. Таким образом, площадь S будет наименьшей вместе с длиной отрезка МК. Но среди отрезков, соединяющих точки двух скрещивающихся прямых СЕ и АВ, наименьшую длину имеет общий к ним перпендикуляр. Нетрудно сообразить, что общим перпендикуляром к указанным прямым является отрезок М'О, соединяющий середину ребра СЕ и диагонали АВ. Действительно, \(\Delta\)AМ'В равнобедренный и поэтому M'O⊥AB. Так как и \(\Delta\)СОE равнобедренный, то M'O⊥СE. Таким образом, наименьшую площадь имеет сечение, делящее ребро СЕ пополам; соответствующая площадь ![]()
Эту же задачу можно решить и иначе, если воспользоваться следующей теоремой: квадрат площади плоского многоугольника равен сумме квадратов площадей его проекций на три взаимно перпендикулярные плоскости. Эта теорема без большого труда доказывается на основании формулы, по которой площадь проекции плоского многоугольника на плоскость равна площади многоугольника, умноженной на косинус угла между плоскостями (см. формулу (1) в решении задачи 230). Считая эту теорему доказанной, обозначим через х длину отрезка СМ (см. рис.). Проекции интересующего нас параллелограмма на плоскости ACD, ECDB и BDN изображены в соответствующем порядке на рисунке, а, б и в.
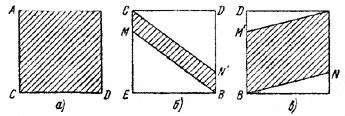
Площади проекций соответственно равны а2, ах, а2—ах, так что в силу упомянутой теоремы S2 = (а2)2 + (ax)2 + (а2 — ax)2 = 2а2 (x2 — ах + а2).
Представив квадратный трехчлен x2 — ах + а2в виде (х —a/2)2 + 3/4 а2 , находим, что наименьшее значение S2 будет иметь при x = a/2, а минимум площади равен
![]()