Окружность радиуса, равного высоте некоторого равнобедренного треугольника, катится по основанию этого треугольника. Доказать, что величина дуги, отсекаемой на окружности боковыми сторонами треугольника, остается при этом постоянной. Будет ли это предложение верно для неравнобедренного треугольника?

Пусть ABC — данный треугольник, АВ = ВС, ВО || АС, О — центр окружности, касающейся AC; D и Е — точки пересечения этой окружности с АВ и ВС.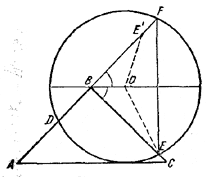

Продолжим АВ до второго пересечения с окружностью в точке F. Докажем, что FE ⊥ BO.

Заметим, что ∠OBF = ∠OBE так как эти углы равны углам при основании АС в треугольнике ABC. Далее BF = BE; действительно, если бы было BF > BE, то, отложив на BF отрезок BE' = BE, мы имели бы равные треугольники ОBЕ и ОВЕ' и ОЕ' = ОЕ, что невозможно, так как точка E' лежит внутри окружности радиуса ОЕ;
аналогично докажем, что невозможно неравенство BF < BE. Но биссектриса ВО в равнобедренном треугольнике FBE должна быть и высотой, что и требовалось доказать.

Поэтому ∠DFE = ¹/₂∠ABC не зависит от положения точки О на прямой ВО. Следовательно, величина дуги DE, половиной которой измеряется ∠DFE, остается при качении окружности постоянной.