К окружности проведены две касательные, которые пересекают в точках А и В прямую, проходящую через центр окружности, и образуют с этой прямой равные углы. Доказать, что любая (подвижная) касательная отсекает на данных (неподвижных) касательных отрезки АС и BD, произведение которых постоянно.

Возможны три случая. Они изображены на рис. 101, а, б, в.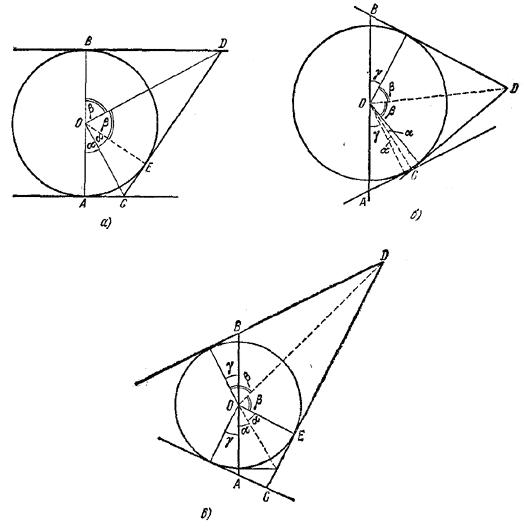

Pис. 101

В первом случае неподвижные касательные параллельны,угол COD = α + β = ^π/₂, поэтому CE • ED = OE², т. е. AС • ВD = r², где r — радиус окружности.

Во втором и третьем случаях, пользуясь обозначениями, легко понятными из рисунка, находим, что α + β ± γ = ^π/₂ т.е. α ± γ = ^π/₂ — β откуда следует, что \(\Delta\)AOC подобен \(\Delta\)BDO и потому

Следовательно,

AC • BD = AO² = r².